发布时间：2022-01-04所属分类：医学论文浏览：1次
摘 要： 摘 要 脑功能网络是分析复杂网络之间连接关系的一种有效方法, 对脑功能障碍分析具有重要意义. 本文基于频域 Granger 因果分析的定向传递函数(DTF), 构建了各频段的脑功能网络. 采用图论方法分析最佳阈值下经颅直流电刺激 (transcranial direct current stimulation, tD
摘 要 脑功能网络是分析复杂网络之间连接关系的一种有效方法, 对脑功能障碍分析具有重要意义. 本文基于频域 Granger 因果分析的定向传递函数(DTF), 构建了各频段的脑功能网络. 采用图论方法分析最佳阈值下经颅直流电刺激 (transcranial direct current stimulation, tDCS) 干预前后孤独症 (autism spectrum disorder, ASD) 儿童脑网络的平均度、全局效率和平均局部效率等特征, 并对比了经颅直流电刺激对孤独症儿童脑功能状态辅助干预效果. 结果发现刺激前组在各频段的图论特征均低于刺激后组(P<0.05), 其中 Theta 频段和低 -beta 频段的局部效率统计性差异显著, 表明在一定程度上 tDCS 干预是 ASD 儿童治疗的有效手段.
关键词 孤独症, 经颅直流电刺激, 脑功能网络, 定向传递函数
2014 年美国疾病控制与预防中心 (Center for Disease Control and Prevention, CDC) 发布最新数据指出：孤独症发病率已经达到了 1：45, 即每 45 个儿童中就有一人是 ASD 患者[1] . 孤独症谱系障碍是一种严重的发育障碍性疾病, 其基本特征是社会交流障碍、语言交流障碍、重复刻板行为. 不典型孤独症则在前述三个方面不全具有缺陷, 只具有其中之一或之二. 不仅对患者本人及其家庭乃至社会都造成极大影响[2] . 对于孤独症儿童, 早发现早干预至关重要[3−4] .
研究者发现 ASD 与脑结构改变及脑功能网络异常的拓扑变化有关, 在 ASD 人群静息态脑电中体现出了这种异常或连接障碍[5] . 孙小棋[6] 通过实验证明孤独症前颞叶和后顶叶的脑电信号呈现出的复杂性明显低于正常, 这一结果表明 ASD 和正常人之间脑电信号存在差异性, 且不同脑区敏感程度不同.Bressler S L 等人[7] 研究表明, 认知是由在大规模网络中运作的分布式脑区的动态相互作用引起的. Murias M 等人[8] 在 2007 年, 通过对 ASD 儿童静息态脑电的研究发现, 在 Theta(3 6Hz) 频率范围内, ASD 组尤其是左侧额叶和颞叶区的相干增强明显. 在较低的 Alpha 范围 (8-10 Hz), ASD 组在额叶区域和额叶与其他头皮区域之间的一致性明显降低. 提示 ASD 患者存在明显的脑连通性异常. 2014 年, Coben R 等人[9] 运用 Granger 因果分析方法计算 ASD 人群的脑网络各通道间的效应连接, 结果表明 ASD 人群的脑功能网络短距离过度连接、长距离连接不足. Green SA 等人[10] 发现孤独症患者大脑网络与正常人相比有改变, 对于这种改变的静息状态连接如何与大脑在信息处理过程中的活动有关的. 2016 年, 孙金秀[11] 基于图论参数对比 ASD 儿童和正常儿童脑网络差异, 结果发现这种差异在高频段更为显著, 且 ASD 儿童的脑网络连接密度更低. 大脑是具有多个层次、多种反馈机制和整合机制的复杂系统, 并且脑功能网络都表现出较其他实证网络更加良好的鲁棒性, 因此, 依据基于图论参数的脑功能网络分析方法, 可以为改善脑功能障碍提供了不同的方向.
神经调节技术早期干预 ASD 是一种有效方法. Schneider HD 和 Hopp JP[12] 将 tDCS 应用于孤独症儿童治疗, 通过修改过的双语测试 (BAT) 对患儿进行语法测试, 结果表明 tDCS 前后差异有显著性意义 (p<0.0005, d65=652.78), 表明 tDCS 干预对孤独症儿童脑功能障碍有一定改善. Amatachaya A 等[13] 对 20 例孤独症儿童进行随机双盲交叉试验, 结果表明进行 tDCS 真性刺激的患儿治疗后儿童孤独症评定量表(children autism rating scale, CARS)和孤独症治疗评估量表(autism treatment evaluation checklist, ATEC)得分均有改善, 而假性刺激组未见改善. 这些研究发现为 tDCS 的临床及科研发展提供理论基础.
采用频域 Granger 因果分析定向传递函数方法建立脑功能网络, 通过计算各导联间因果连接矩阵, 构建 Theta 频段、Alpha 频段、低 -Beta 频段、高 -Beta 频段和 Gamma 频段五个频段的脑功能网络. 基于脑功能网络, 分析经颅直流电刺激对于孤独症儿童干预效果.
1 脑功能网络建立
1.1 频域 Granger 因果分析方法
由于 ASD 患儿年龄较小、认知水平和任务配合程度低, 基于静息态脑电信号分析脑功能状态分析更可行、更具优势[14] , 同时脑电信号具有成本低[15] 的特点, 因此本文基于脑电信号构建孤独症儿童脑功能网络.
网络连接表示网络中各个节点之间相互关系或相互作用, Granger 因果关系检验方法不需要先验知识, 较其他方法更具优势. Granger 因果分析方法基于二元自回归模型, 考虑 EEG 信号的频域特征明显, 本文基于多元自回归模型的频域 Granger 因果分析方法, 即定向传递函数(Directed Transfer Function, DTF)方法[16] , 建立脑功能网络, 进而分析刺激前后两组多通道脑电的功能连通性.
其中, MVAR 模型的阶数 p 通过贝叶斯信息准则(Bayesian Information Criterions, BIC)计算, 并调用 arfit 工具箱函数实现[17];通过调用 He B 等人[18] 开发的 eConnectome 工具箱函数实现 DTF 的计算以构建脑网络.
1.2 复杂脑网络的图论特征分析
图论(GraphTheory)是研究复杂脑网络拓扑结构的重要数学工具. 通过图论分析发现人脑功能网络呈现小世界网络特征[19] . 基于图论的复杂脑网络分析可以从宏观的视角分析人脑, 更好的描述脑功能网络的拓扑特性.
大脑的功能网络构建[20] , 首先将电极或通道作为网络” 节点”, 令电极或通道之间的连接定义为” 边”, 从而构建脑网络, 进一步运用图论参数对复杂脑网络进行探究.
1.2.1 节点度
度是邻接到某节点的边或弧的数目, 节点度可以衡量该节点在网络中的重要程度.
1) 入度和出度
在复杂网络中, 有向图的度有入度、出度之分. 节点的入度, 是指以该节点为终点的边的数目, 与该节点受其他节点的影响程度正相关. 节点的出度, 是指以该顶点为起点的边的数目, 与该节点对其他节点的影响程度成正比. 入度如式 6 所示, 出度如式 7 所示.
2 试验及数据处理
2.1 数据采集
随机抽取 10 名 ASD 儿童 tDCS 干预前后脑电数据, 其中 8 名男孩, 2 名女孩, 年龄在 4∼7 岁, 平均年龄为 5.76±0.24. 试验协议通过伦理审查委员会批准, 且遵从受试者自愿参与的原则, 试验人员告知受试者及其家人试验流程及要求, 在家长或监护人同意情况下签订知情同意书. 试验将 tDCS 干预的刺激点选在背外侧前额叶的位置, 周期设定为五周, 每周两次干预, 每隔两天做一次, 共十次. 试验分为两部分：脑电数据采集和行为数据采集. 第一次干预之前和第十次干预之后需要进行脑电数据采集和行为数据采集. 脑电信号采集时, 要求受试者在安静的房间内, 坐在舒适的椅子上, 以保持安静状态, 实验开始前, 要求受试者安静 3 4 分钟, 以便进入放松状态, 然后进行五分钟的脑电信号采集, 脑电数据采集完成后, 休息两分钟, 进行时长 20 分钟的神经调节干预, 在干预的五周内, 受试者均不参与除本研究中干预以外的任何物理干预和药物治疗.
试验采用美国 EGI 公司生产的 128 导联的脑电采集设备(HydroCel Geodesic Sensor Net, Electrical Geodesics, Inc, Eugene, OR), 使用 Net Station4.5.2 进行时长 5 分钟的静息态脑电采集, 将头上的顶点 vertex(Cz)的电极作为参考, 同时设定每个电极小于 50KΩ 的阻抗值, 参考电极和双侧乳突处电极低于 10KΩ, 采样率为 1000Hz. 要求受试者在安静的房间内, 舒服地坐在椅子上, 期间要保持安静状态, 尽量避免或减少外界干扰, 记录受试儿童在保持清醒和放松状态下的 16 导联静息态脑电数据.
行为数据需要家长或长期照顾受试者的人针对孩子近期的状况填写孤独症行为量表 (Autism Behavior Checklist, ABC), ABC 量表不受性别年龄的限制, 家长根据孩子近期的行为表现进行量表填写, 量表评估具有一定的主观性.
2.2 数据预处理
由于采集到的 EEG 中还包括其他一些噪声信号, 如随机噪声和伪迹. 通常我们所接触到的伪迹有工频干扰、心电伪迹、肌电伪迹、眼电伪迹、电磁干扰等. 因此在进一步处理数据前, 去噪是非常必要的[21] .
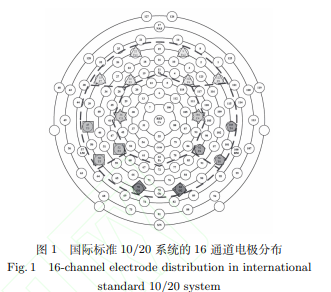
(1) 从 128 个通道里按照国际标准的 10/20 系统选出本文所需要的 16 个通道, 分别为额区 FP1、FP2、F3、F4、F7、F8、T3、T4、T5、T6、C3、 C4、P3、P4、O1、O2, 如图 1 所示, 这些通道分别在额叶, 顶叶, 枕叶, 左颞叶和右颞叶等 5 个脑区;
(2) 进行坏通道替换, 如果我们进行数据分析的所需通道中有存在问题的, 那么将用该通道周围的通道数据进行平均所代替;
(3) 对 16 个通道的脑电数据降采样至 128Hz;
(4) 去除存在的伪迹信号;
(5) 将脑电数据从稳定位置开始, 截取为 30 段,每段 1 秒;
(6) 将预处理的数据改为工具箱可用的形式, 其中通道数为 16, 各通道采样点数为 1000, 采样率为 1000.
3 试验结果与分析
3.1 计算因果效应连接
MVAR 模型的阶数 p 根据贝叶斯信息准则确定. 通过计算 DTF 连接矩阵, 分别对 Theta 频段(4-8Hz)、Alpha 频段(8-12Hz)、低 -Beta 频段(12-24Hz)、高 -Beta 频段(24-30Hz)和 Gamma 频段(30-60Hz)进行探究. 其中, 每个 DTF 矩阵大小均为 16 × 16, 矩阵元素 DT Fij 定义为从导联 j 到导联 i 的因果连接值.
因为脑电数据截取可能出现影响最终结果的误差, 所以本文中每位 ASD 儿童经预处理后的静息态脑电数据截取为 1 秒一段, 共 30 段的脑电数据, 并分别计算其 DTF 矩阵. 因此, 五个频段的刺激前后每组均有 300(10 × 30)个 DTF 矩阵, 有刺激前后两组, 共 3000(10 人× 30 秒× 5 段× 2 组)个 DTF 矩阵.
刺激前后两组受试儿童静息态脑电 5 个频段的平均 DTF 矩阵分别如图 2 和 3. 矩阵中元素代表通道 j 到通道 i 间的连接值, 可以看出刺激后组脑网络连通性要优于刺激前组.
分别计算五个频段下刺激前后两组每个 DTF 中全部元素之和, 得到全脑范围 DTF 矩阵的总和, 最终计算结果如表 1 所示. 经 t 检验, 刺激前组的全脑 DTF 总和在 Theta 频段、Alpha 频段、低 -Beta 频段、高 -Beta 频段和 Gamma 频段下均低于刺激后组, 并具有统计性差异(p<0.005), 其中在 Alpha 频段、低 -Beta 频段和 Gamma 频段刺激前后两组具有显著性差异(p<0.001).
3.2 最佳阈值选取
运用频域 Granger 因果分析方法构建脑网络时, 需要选取最佳阈值 T, 使得 DTF 矩阵转化为二值有向图. 将 DTF 矩阵元素大于 T 的位置置为 1, 表示对应节点之间存在因果连接, 小于 T 的位置置为 0, 表示对应节点之间不存在因果连接. 因为节点本身之间不存在因果关系, 所以连接矩阵的对角线位置置为 0.
阈值的选择对复杂脑网络有一定影响：过高的阈值下网络连接过少, 从而破坏网络的连通性;但是阈值过低将导致网络中存在大量虚假连接, 使得刺激前后两组差异性不显著. 由图 4 所示的间接因果关系示意图, 假设 A 节点对 B 节点有直接影响, B 节点对 C 节点有直接影响, 而 A 节点对 C 节点并没有直接影响, 但通过 B 节点, A 和 C 之间产生了间接的、虚假的连接关系. 因此, 最佳阈值的选择至关重要, 本文在较大阈值范围 0.001≤T≤0.1, 步长为 0.001 的情况下观测在不同阈值下受试儿童刺激前后脑网络的图论参数统计性差异.
将给定的阈值 T 带入计算得到的所有 DTF 矩阵中, 经计算得到二值化后的连接矩阵, 最终表示有向网络, 进而再计算出各个频段的图论参数.
平均度与脑网络的稀疏程度成正比, 全局效率反映网络在全局范围内信息传递和信息处理能力, 网络的局部效率则表示网络节点的紧凑程度, 即局部信息传输能力. 分别计算两组受试儿童 Theta 频段、Alpha 频段、低 -Beta 频段、高 -Beta 频段和 Gamma 频段在不同阈值取值下, 脑网络的平均度、全局效率和局部效率. 阈值取值范围为 0.001≤T≤0.1, 步长为 0.001.
采用配对样本 T 检验分别比较刺激前后两组在不同频段上因果网络的平均度、全局效率和局部效率. 以 Gamma 频段的平均度为例, 当 T=0.001 时, 刺激前后两组的平均度分别为 29.88±0.038, 29.88±0.007, 平均每个节点与 29 个左右的节点相连接, 说明阈值过低;当 T=0.1 时, 刺激前后两组平均度分别为 4.10±0.169, 4.14±0.102, 平均每个节点与 4 个左右节点相连接, 即网络过于稀疏, 阈值过高. 因此判定该阈值取值范围中, 存在较合理的最佳阈值.
基于 DTF 矩阵值, 分别构建刺激前后两组在 Theta 频段、Alpha 频段、低 -Beta 频段、高 -Beta 频段和 Gamma 频段的因果网络. 各个频段在各阈值下, 网络的平均度、全局效率、平均局部效率阈值统计表分别如表 2、3、4、5、6 所示.
最佳阈值的选取应考虑：(1)尽可能的体现出刺激前后的网络差异;(2)在合理的网络稀疏程度范围, 尽量保证网络没有孤立节点. 综上所述, 根据表 2、3、4、5、6, 得到各个频段的阈值以及对应图论参数的显著性如表 7 所示.
3.3 最佳阈值下的统计分析
各个频段在最佳阈值下, 网络的平均度统计表如表 8 所示. 统计分析结果显示, 刺激前组的脑网络平均度在五个频段下均低于刺激后组, 并具有统计性差异, 但是 Alpha 频段不如 Theta 频段、低 -Beta 频段、高 -Beta 频段和 Gamma 频段统计性差异显著.
刺激前后两组不同频段下的脑网络的全局效率如表 9 所示. t 检验后, 发现两组数据在各频段下具有统计性差异且刺激前组的脑网络全局效率在五个频段下均低于刺激后组, 其中 Gamma 频段比 Alpha 频段、Theta 频段、低 -Beta 频段和高 -Beta 频段的差异显著性更高.
如表 10 所示, 为刺激前后两组在各频段下的脑网络的局部效率值, t 检验后, 刺激前组的脑网络局部效率均低于刺激后组, 并且都具有统计性差异, 其中 Theta 频段和低 -beta 频段更具有显著性差异
4 结论
本文基于定向传递函数方法, 构建孤独症儿童经颅直流电刺激前后脑功能网络. 基于图论复杂网络分析方法对所构建的因果网络进行量化分析, 计算脑功能网络 DTF 矩阵值. 分析选择最佳阈值, 将 DTF 矩阵转化为二值有向图, 研究网络的平均度、全局效率和局部效率等网络特性参数, 经 t 检验统计分析两组数据统计性差异. 探究经颅直流电刺激干预对孤独症儿童脑功能网络的影响.
网络平均度与网络的稀疏程度正相关, 全局效率反映网络在全局范围内信息传递和信息处理能力, 网络的局部效率反映了网络局部信息传输能力. 通过研究分析发现刺激前组在各频段的平均度、全局效率和局部效率均低于刺激后组(P<0.05), 说明经颅直流电刺激干预后孤独症患儿的脑网络稀疏程度、全局范围和局部范围的信息传输能力都得到了一定的改善, 其中局部效率统计性差异最为显著, 尤其是在 Theta 频段和低 -beta 频段的局部效率, 提示 ASD 患儿的脑功能网络的局部连接能力可以通过 tDCS 干预得到较为明显的提升. 行为数据通过 ABC 量表分析, 结果表明 ASD 儿童的 ABC 量表得分整体下降, 在感觉、交往、运动、语言和自我照顾能力五个方面均有改善, 尤其在语言能力方面改善最大, 效果最为突出, 干预后 ASD 儿童表达能力有所改善, 对事物的认知和理解能力增强, 交往能力也随之增强, 与他人的眼神交流增多, 且易怒性降低, 整体水平均升高. 结合脑电数据和行为数据分析, tDCS 对改善 ASD 症状有一定的作用, 因此在一定程度上可以作为干预 ASD 的有效手段, 给 ASD 儿童早期干预治疗提供一条思路.
就现有的研究而言, 基于频域 Granger 因果分析构建的脑功能网络改变并不能完全反映 ASD 症状的改善效果, 还需要进一步研究. 由于 ASD 儿童的脑功能会随着年龄的变化而改变, 未来仍需探究不同年龄段 ASD 儿童经过 tDCS 干预后的脑功能网络变化和临床症状, 以助于进一步证实 tDCS 辅助干预对 ASD 儿童的治疗效果.——论文作者：李 昕 1, 2 王 欣 1, 2 安占周 1, 2 蔡二娟 1, 2 康健楠 3
SCISSCIAHCI
