0
发表咨询在线!

发布时间:2022-01-06所属分类:农业论文浏览:1795次
摘 要: 摘要:在采样数据的基础上, 应用地统计学的理论与方法, 尝试研究太湖水质参数空间分布特性.结果显示, 太湖水质参数的空间结构变异性是客观存在的, 各水质参数都具有块金效应;对太湖水质参数进行克立格插值, 并进行污染水平分类, 可以提供更为直观的水环境信息.研究结果

摘要:在采样数据的基础上, 应用地统计学的理论与方法, 尝试研究太湖水质参数空间分布特性.结果显示, 太湖水质参数的空间结构变异性是客观存在的, 各水质参数都具有块金效应;对太湖水质参数进行克立格插值, 并进行污染水平分类, 可以提供更为直观的水环境信息.研究结果对太湖的水环境管理有一定的参考价值.
关键词:太湖;水质参数;地统计学
太湖水质污染目前已严重影响了整个流域的可持续发展, 并对人们的身体健康造成潜在的危害 .治理太湖、保护太湖已成为刻不容缓的任务.了解湖泊水质参数空间分布特征是进行太湖环境评价的重要前提 .
但是太湖水质参数的空间分布是不均匀的, 由于这种空间变异性既具有随机性又具有结构性, 因此用传统方法进行太湖水质参数空间分布的研究具有明显的局限性, 地统计学的出现为解决这个问题提供了新的方法.本文应用地统计学的理论与方法, 尝试在太湖水质参数空间分布研究方面做新的探讨 .
1 太湖概况
太湖是我国的五大淡水湖之一, 位于长江三角洲 .湖面面积是 2460 km 2 , 实际水面面积为 2338 km 2 [ 1] .整个流域面积涉及上海市 、江苏省、浙江省等省市 .太湖地区是我国经济最发达的地区之一, 也是人口最密集的地区之一 .在经济高速发展的同时, 在资源、环境等方面也付出了巨大的代价, 造成了生态系统的严重破坏和环境质量的下降, 尤其是人类活动给太湖造成的水质污染, 产生了水质性资源短缺及太湖生态环境的严重破坏
2 地统计学在太湖水质研究中的应用
2.1 地统计学及其在环境研究中的应用
地统计学( Geostatistics) 是为解决矿床从普查勘探 、矿山设计到矿山开采整个过程中各种储量计算和误差估计问题而发展起来的, 因此得名地统计学, 现在已发展成为能表征和估计各种自然资源的工程学科 [ 2] .近几年, 地统计学在环境科学中得到了广泛的应用, 已发表的研究如Burgess T .M . [ 3] 、Burrough P .A . [ 4, 5] 、沈思渊 [ 6] 、王学军 [ 7] 等 .但是, 目前的研究主要集中在土壤科学方面, 而地统计学在水环境科学, 尤其是湖泊环境中的应用, 在国内还鲜有报道.
2.2 数据采集与处理
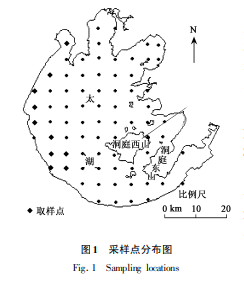
在采样监测中, 考虑到湖岸线和湖中岛的影响, 在太湖中均匀布置共 75 个采样点 .采样点分布见图 1 .采样时间为 1999 年 11 月 4 日, 我们委托国家环保局太湖流域环境监测网中心站进行采样监测 .采样和样品的分析根据国家环境有关规范进行 .在监测中主要考虑了叶绿素 a ( chlorophyll a, 简称 chl-a ) 、总悬浮物( suspended sediment, 简称 SS ) 、透明度( secchi depth, 简称 SD) 3 种水质参数 .
本研究用 Grubbs 法 [ 8] 进行了异常值检验, 为减少信息损失, 显著性水平取 5 %, 仅有少量异常值被剔除.
2.3 太湖水质参数的空间结构分析( 以总悬浮物为例)
结构分析的目的是建立一个变差函数的理论模型, 用它来定量地概括太湖水质参数的全部有效的结构信息, 表征此变量的主要结构特征 [ 9] .并在此模型的基础上作进一步的地统计学研究( 如进行克立格估计和条件模拟等) .因此, 结构分析是应用地统计学研究太湖水质参数空间分布中非常重要的一步 . 图2 总悬浮物的变差曲线图 Fig .2 Variogram curve of SS
2.3.1 确定曲线类型 根据实验变差函数 [ 10] 的计算公式可以得到总悬浮物的变差函数曲线图( 图 2) .从图2 中可以看出, 总悬浮物区域化变量的变差散点图可能是球状模型曲线、指数模型曲线或高斯模型曲线 [ 11] 中的一种, 为了便于比较, 分别对线性有基台值模型 、球状模型 、指数模型和高斯模型进行了参数的最优估计 .
2.3.2 参数最优估计 理论模型最优拟合中最重要的一步是对模型中的参数进行最优估计 .变差函数的理论模型主要是曲线模型, 将曲线模型经过适当的变换, 化为线性模型, 然后用最小二乘法原理进行未知参数的估计.对于球状模型 、指数模型和高斯模型而言。0
2.3.3 最优模型的判断和检验 在模型间的比较时, 选用了残差平方和( Q) 、标准误差( S ) 和决定系数( R 2 ) 等参数, 计算结果见表 1 .从表 1 可以看出, 在 4 个理论模型中, 无论是残差平方和还是标准误差都是球状模型最小, 而球状模型的决定系数又是最大的.尽管它们之间的块金常数和基台值都基本相同, 选择球状模型作为太湖水质参数总悬浮物的变差函数理论模型是比较合适的.这个理论模型除了具有较高的拟合精度外, 对变程以内的模拟可以得到满意的结果.
另外, 还需要对回归模型进行显著性检验, 检验所建立的球状模型的回归方程与回归曲线是否是显著的.通过检验, 球状模型在变程内的拟合是显著的.
2.3.4 结构分析结果 对在太湖中监测的 3 种水质参数进行球状理论模型拟合, 拟合结果见表2 .
2.4 太湖水质参数的空间分布
2.4.1 克立格法是空间插值最优方法 地统计学主要包括空间结构分析和空间插值( 克立格法) 2 部分 [ 12] .克立格法是基于这样一种理解, 即用于推断的研究对象( 如总悬浮物) 的已知值之间相互不是完全独立的, 而是存在着一定的相关关系 .这种相关性既随数据点之间的距离变化, 也随方向变化, 并可用变差函数来表征这种区域化变量的空间结构性 [ 13] .克立格法是以无偏为约束, 寻求估计方差最小的一种插值方法, 是最优空间插值方法 [ 14] .
从以往的研究 [ 15] 可以看出, 克立格插值方法的估计误差均值和估计误差方差两项指标均最小, 这就表明了克立格插值方法在太湖的实际应用中确比传统空间插值方法有着更强的有效性、最优性和无偏性.
2.4.2 插值结果及图形显示 应用地统计学就是为了更好地描述水质参数在太湖中的分布状况 .应用克立格法的最优插值原理与方法, 以太湖湖岸线为边界, 对水质参数进行整个太湖插值生成水质参数在太湖中的等值线 .按照湖泊富营养化划分标准, 参照前人作过的工作 [ 16, 17] , 对等值线整理并用图形显示可生成水质参数在太湖中的分布图.由于篇幅所限, 这里仅给出总悬浮物在整个太湖中的分布状况( 图 3) .
从图 3 中可以明显地看出总悬浮物在整个太湖中的空间分布状况, 这样比零散的采样数据更直观 、有效, 更有利于人们的分析和研究, 有助于找出太湖污染的根源 .对于不同的区域采用不同的措施, 加以解决 .
3 结论
太湖中水质参数分布具有结构性和随机性双重性质, 具有空间变异性 .水质参数的这种特点, 决定了用经典统计学描述太湖水质参数的空间分布具有一定的局限性, 而地统计学则可以避免这种缺陷.在地统计学的应用中, 相对于线性有基台值模型 、球状模型 、指数模型和高斯模型等而言, 球状模型是最优的理论模型, 能较好地拟合变差曲线, 同时拟合结果是显著的 ;应用结构分析的结果, 根据克立格最优插值结果可以生成太湖水质的评价图, 为太湖的治理提供有用的信息 .事实证明, 在太湖水质参数研究中, 地统计学可以充分利用水质参数的空间信息, 为太湖水质研究开辟了一条新的方向.作为一种研究手段, 此种方法可以推广到其它湖泊研究中.——论文作者: 刘瑞民 1 , 王学军 1 , 郑 一 1 , 李 莹 1 , 江耀慈 2 , 周修炜 2
参考文献:
[ 1 ] 中国环境监测总站, 太湖流域环境监测网中心站.太湖水环境质量报告[ R] .无锡:中国环境监测总站, 太湖流域环境监测网中心站, 1999.1—2
[ 2 ] 儒尔奈耳 A G, 尤日布雷格茨 C H J.( 侯景儒, 黄竞先, 杨尔煦, 等译) 矿业地质统计学[ M] .北京:冶金工业出版社, 1982.1—5
[ 3] Burgess T M, Webster R.Optimal interopolation and isarithmic mapping of soil properties.Ⅱ .Block kriging [ J] .J Soil Sci, 1980 ( b) , 31:333—341
[ 4 ] Burrough P A.Multiscale sources of spatial variation in soil.Ⅰ .The application of fractal concepts to nested level of soil variation [ J] .J Soil Sci, 1983( a) , 34:577—597
[ 5 ] Burrough P A.Multiscale sources of spatial variation in soil .Ⅱ .A non-brownian fractal model and its application in soil survey [ J] .J Soil Sci, 1983( b) , 34:599—650
[ 6 ] 沈思渊.土壤空间变异研究中地统计学的应用及其展望[ J] .土壤研究进展, 1989, 2:11—24
[ 7 ] 王学军, 邓宝山, 张泽浦.北京东郊污灌区表层土壤微量元素的小尺度空间结构特征[ J] .环境科学学报, 1997, 17 ( 4) :412—416
[ 8 ] 陶 澍.应用数理统计方法[ M] .北京:中国环境科学出版社, 1994.51—56
[ 9 ] 侯景儒, 尹镇南, 李维明, 等.实用地质统计学[ M] .北京:地质出版社, 1998.36—44
[ 10] 孙洪泉.地质统计学及其应用[ M] .徐州:中国矿业大学出版社, 1990.80—87
[ 11] 戴维M .( 孙惠文, 刘承祚译) 矿产储量的地质统计学评价[ M] .北京:地质出版社, 1989.122—134
[ 12] 王政权.地统计学及在生态学中的应用[ M] .北京:科学出版社, 1999.102—149
[ 13] 张 征, 张人权, 徐恒力, 等.定量预测岩溶含水介质渗透性空间分布的克立格法[ J] .中国岩溶, 1995, 14 ( 3) :1—8
[ 14] 王仁铎, 胡光道.线性地质统计学[ M] .北京:地质出版社, 1988.123—126
[ 15] 刘瑞民, 王学军.湖泊水质参数空间优化估算的原理与方法[ J] .中国环境科学, 2001, 21( 2) :177—179
[ 16] 黄漪平, 范成新.太湖富营养化综合评价[ A] .中国科学院南京地理与湖泊研究所集刊[ C] .北京:科学出版社, 1993. 18—26
[ 17] 黄漪平, 范成新, 袁静秀, 等.太湖水质现状及变化趋势[ A] .中国科学院南京地理与湖泊研究所集刊[ C] .北京:科学出版社, 1993.27—35
声明:①文献来自知网、维普、万方等检索数据库,说明本文献已经发表见刊,恭喜作者.②如果您是作者且不想本平台展示文献信息,可联系学术顾问予以删除.

SCISSCIAHCI