发布时间:2021-12-29所属分类:电工职称论文浏览:1次
摘 要: 摘要:随着风电大规模并网,电力系统逐渐发展为低惯量系统,广泛推广风电机组转子惯性控制技术对于提高系统的频率稳定性具有重要意义。文中通过对双馈风电机组和火电机组调频特性的分析以及对双馈风电机组等效惯性常数的研究,提出了风-火系统模糊自适应虚拟惯量控制策
摘要:随着风电大规模并网,电力系统逐渐发展为低惯量系统,广泛推广风电机组转子惯性控制技术对于提高系统的频率稳定性具有重要意义。文中通过对双馈风电机组和火电机组调频特性的分析以及对双馈风电机组等效惯性常数的研究,提出了风-火系统模糊自适应虚拟惯量控制策略。首先根据风电机组运行工况和系统风电渗透率模糊动态决策出了风电场调频比例系数,其次基于风电机组辅助惯性控制微分系数与风电机组等效惯量常数的关系和风火联合增量系统模型整定了风电机组虚拟惯性控制参数的变化范围,最后设计算例验证了所提自适应调频控制策略的有效性。仿真结果表明该策略不仅使得风电机组在各种运行工况下均能够提供可靠的有功支撑,还保证了调频过程中风电机组的稳定运行,提高了系统的频率稳定性。
关键词:低惯量系统;双馈风电机组;等效惯量常数;模糊控制;自适应虚拟惯量
0 引言
近年来,随着“两个替代”战略的推广实施,系统中风电渗透率不断提高[1]。然而大规模风电的接入将明显降低电力系统的抗扰动能力和调频能力[2-3]。为了削弱含高渗透风电系统的低惯量特性,国内外最新发布的电网导则均要求并网风电机组能够有参与系统调频和备用的能力[4]。
目前,国内外学者对风电机组参与调频的控制策略进行了大量的研究。风电机组的调频控制,主要通过采用附加控制结构改变自身或储能模块的有功输出来响应系统频率变化[5]。具体实现方法包括转子惯性控制[6-8]、功率备用控制[8-9]和综合协调控制[10-11]以及储能型虚拟同步机技术[12]等,风电机组均能够有效的参与系统调频。其中,风电机组的转子惯性控制是通过调节风电机组的转子转速以释放出旋转动能来实现的,其能够快速地提供惯量支撑以抑制系统频率恶化,在有效改善系统调频性能的同时有较好的经济性[13-14]。为了使风电机组的转子惯性控制能够适应电网运行状态,文献[15-16] 根据系统频率变化情况提出了跟踪系统频率状态动态调节惯性控制参数的调频策略,极大地挖掘了风电的调频潜力,改善了电网频率特性。同时,风机转子中的动能有限,若一味追求风电机组参与系统调频的能力,系统容易出现频率的二次跌落事件。基于此,文献[16-18]依据风机所处环境和自身运行条件提出了变参数控制方法,使得风电机组能够稳定的参与调频,避免了系统频率的二次跌落,改善了系统的频率响应能力。然而这些控制方法较为繁琐,难以适应工程应用,且没有考虑风电机组控制本身的稳定性。
针对风火联合系统的协调调频控制,在风火调度层,首先需要解决的是风电场需要分担的功率缺额比例。文献[16]以风速分区为基础,进一步基于模糊逻辑控制方法实现了风电场与储能系统的灵活配合,实时决定了风电场的短期频率响应有功增量,提高了系统频率稳定性;文献[19]则基于风电机组分区,在确定风电场和火电机组参与调频的功率参考值的基础上,进而对风电场调频功率进行了动态分配。然而,上述文献均是在风电渗透率不变的场景下所进行的研究,并没有考虑不同风电渗透率工况下调频控制方案的适用性。
综上所述,本文在定位辨析风电、火电调频特性的基础上,探究适用于不同风电渗透率工况下的模糊自适应虚拟惯量控制方案。在风火调度层,基于模糊控制根据风电机组运行工况和风电渗透率提出动态决策风电场调频比例系数的模糊控制策略;在风电机组层,基于风机有效旋转动能计算得出风电机组的等效惯性常数,分析最大等效惯性常数与转子转速的关系,基于惯性控制微分系数与等效惯性常数的关系和风火联合增量系统模型提出风电机组层模糊虚拟惯量控制方案。仿真结果表示所提策略有效改善了系统的频率稳定性,提高了系统运行的安全稳定。
1 风电机组虚拟惯量控制
1.1 风火调频特性辨析
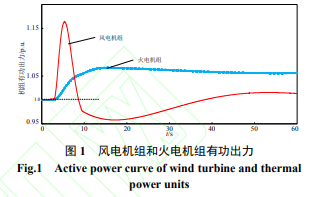
研究含高渗透风电系统的调频控制,首先要分析、定位风电机组与火电机组参与调频的调频特性和调频任务。目前,双馈风电机组 (doubly- fed induction generator, DFIG) 是风电场的主流机型,因此本文以 DFIG 作为研究对象,DFIG 参数取值见文献[6]。此外,为使 DFIG 能够表现出较稳定的虚拟惯量,本文依据风速变化将 MPPT 运行曲线划分为如文献[20]所示的四个区间。考虑到 DFIG 在四个区间的运行特性,本文仅研究运行在 MPPT 区间的 DFIG 及风-火系统的模糊虚拟惯量控制。图 1 为算例系统发生频率跌落时风电机组和火电机组的有功出力曲线。
由图 1 可知,由于风电机组是经电力电子器件并网出力的,对电网表现出较小的惯性时间常数,因此其能够在频率扰动的初始迅速提供较大的有功支撑,但持续时间较短,在本系统中仅约为 4s,且在频率恢复过程中会增加额外的调频需求,导致当系统中风电出力占比较高时,易出现较严重的二次频降现象[14]。而火电机组具有较大的惯性时间常数,虽然不能快速阻尼系统频率变化,但其能够在较长周期的调频过程中维持稳定的出力,保证了系统频率的稳定。
综上所述,在参与系统调频过程中,应当充分发挥风电场调频快速性和火电机组调频持续性的特点,将其分别作为快速、暂态和持久、稳定的有功电源。同时应注意到当系统中风电渗透率较高时,为避免出现严重的二次频降现象,在频率恢复阶段应尽量削弱系统的等效惯性和阻尼作用,以加速系统频率的恢复。
2 基于 DFIG 有效动能的风-火系统模糊虚拟惯量控制
2.1 DFIG 有效动能
综合考虑风电机组调频前后的物理特性,DFIG 有效动能的变化包括两部分[18],如图 2 所示,有效动能的变化受机组转速变化范围约束。DFIG 有效动能可以用风电机组等效虚拟惯性常数 Hwvir 表示,如式(4)所示,式中变量含义见文献[18]。
2.2 风-火系统模糊虚拟惯量控制
为了提高风-火系统的调频性能,本文依据风电场运行条件以及频率状态确定了系统的有功增量,实现了风电、火电机组调频特性的灵活配合。
2.2.1 风火调度层控制策略
为充分利用风电场的调频容量并适应不同风电渗透率,在风火调度层,利用模糊逻辑控制器 FIS1 确定风电场的调频比例系数 Kw,具体控制结构如图 2 所示。对于 FIS1,其输入量为风电渗透率 w (0.02~1)与风资源条件 (当地的平均风速) Vw(6~10m/s),输出量为风电场的调频比例系数 Kw(0~1),其与风电场调频能力的强弱是正相关的。 FIS1 根据当前系统运行工况下并网风电机组参与调频的能力来动态确定 Kw,进而决定了系统频率响应过程中风电场承担的出力增量,如式(2)所示。
确定 FIS1 的输入与输出变量对应关系及隶属度函数曲线如附录 A 图 A2 所示。FIS1 在充分利用风电场调频潜力的同时避免了对风电场调频的依赖,保证了系统频率的稳定性。基于此建立了如表 1 所示的模糊逻辑规则表,该规则表体现了下述的推理原则:当风速 Vw 非常小且风电渗透率 w 较小时,则输出 Kw要尽可能小;当风速 Vw 较小且风电渗透率 w 较大时,则输出 Kw 较大;当风速 Vw 较大且风电渗透率 w 较小时,则输出 Kw 较大;当风速 Vw 较大且风电渗透率 w 较大时,则输出 Kw 非常大。综上得到了模糊逻辑系统基于 Mamdani 型的模糊控制输出结果如图 4 所示。
2.2.2 机组层控制策略
本节欲建立风电机组层的模糊虚拟惯量控制策略,考虑到风电机组控制参数的实时改变可能对系统整体稳定性产生影响[15,21],针对运行在 MPPT 区间的 DFIG 建立图 5 所示的风火联合增量系统模型,以整定控制参数的合理变化范围,模型中初始化参数取值见附录 A 表 A1。在额定风速以下 (Vw=9m/s),设定惯性控制参数 Kdf 和 Kpf 均为 1,不断改变增益系数 Kdfp 和 Kpfp 的取值,进行频域特征值分析,绘制出影响系统阻尼特性的主导特征根的移动轨迹如图 6 所示。
对图 6 进行分析可知,当 Kpfp 较小时,特征根1 会出现正值,由式(3)可知这是因为 Kpfp 的大小与系统阻尼有关,Kpfp 过小会减小系统阻尼,导致系统稳定性不佳,当 Kpfp 增大时特征根1 向左半平面移动,系统稳定性得到改善;当 Kpfp较大时,特征根2 会减小直至移动到右半平面,这是由于 Kpfp 过大会导致风电机组控制本身的失稳。同理分析可知,特征根3 和4 的变化特性同样会限制 Kdfp 的变化范围。由此可得,①系数 Kpfp 取值范围为(- 7~19);②系数 Kdfp 的取值范围为(-9~11)。因此,将以上取值范围的子集作为虚拟惯量控制参数的变化范围能够保持系统稳定性不受影响。
为达到根据系统频率波动状态动态调节系统等效惯量和阻尼且保持风电机组控制稳定性的要求[15,18],本文基于惯性控制系数 Kdf 与等效惯性常数 Hwvir 的关系和风火联合增量系统模型提出风电机组层模糊虚拟惯量控制,控制结构如图 7 所示。
如图 7 所示,在机组控制层,利用风电机组模糊逻辑控制器 FIS2 动态调节惯性控制参数,以改变系统等效惯量和阻尼。对于 FIS2,取系统频率偏差f ( - 0.005~0 p.u.) 和 频 率 变 化 率 d dt f ( - 0.012~0.012 p.u./s)[22]为输入量来有效区分系统频率波动状态,输出量为惯性控制微分系数 Kdf (0~1) 及比例系数 Kpf (-6~6)。FIS2 的输入与输出量对应关系及隶属度函数曲线如附录 A 图 A3 所示。
FIS2 根据系统频率变化实时调整风电机组的有功输出,动态模拟同步发电机的功频下垂和惯量响应特性,有效补偿了风火系统的等效惯量和阻尼,基于此建立了如表 2 所示的逻辑规则表。
FIS2 体现的推理原则为:当系统频率偏差f 较小且系统频率变化率 d dt f 绝对值较小时,则输出 Kdf要尽可能小,Kpf 为负值且绝对值尽可能大;当系统频率偏差f 较大且系统频率变化率 d dt f 为正值时,输出参数 Kdf 要尽可能小,Kpf 为负值且绝对值尽可能大,使得系统频率尽快恢复稳定;当系统频率偏差f 较大且系统频率变化率 d dt f 为负值时,输出参数 Kdf 要尽可能大,Kpf为正值且绝对值尽可能大,以减小系统频率波动。综上得到了系统基于 Mamdani 型的输出结果如图 8 所示。
3 算例分析
为验证文中所提风-火系统模糊虚拟惯量控制的有效性和风电机组的自适应控制效果,建立附录 B 图 B1 所示的两区域系统模型。区域Ⅰ由 9 台火电机组构成,单台机组额定有功为 300MW,其中机组参数按附录 A 表 A1 取值。区域Ⅱ为风电场,采用单机等值模型,装机容量为 400MW,风机均运行在 MPPT 区间。负荷消耗的额定功率 PL 为 1600MW,通过设定负荷突增量来模拟频率跌落事件。本文以保持旋转备用不变,进行风火容量等比例置换来改变系统的风电占比 w 。仿真验证项目包括:
1)维持系统风电渗透率不变,将区域Ⅱ中风电机组按风速进行分组,设定发生一定的功率扰动,验证所提协调调频策略的可行性,校核风电机组的控制效果。
2)在不同风电渗透率工况下,区域Ⅱ中风电机组的运行风速相同,设定发生同样的功率扰动,校核系统的调频性能,验证所提模糊协调策略的鲁棒性。
3.1 同一风电渗透率工况下系统调频效果分析
设定系统风电渗透率 w 为 25%,根据运行风速,将区域Ⅱ中风电机组按每间隔 1m/s 原则从高到低分为 4 个风速段(R1~R4),每个风速段的机组出力和均为 100MW。仿真 t=2s 时,系统负荷突然增加 22MW,仿真结果如图 9 所示。
如图 9(a)所示,当系统发生功率扰动后,风电场参与调频使得系统频率最大偏差减小,频率回复正常值的持续时间增长。对比风电场不参与调频和风电场以文献[9, 15]采用的转子惯性控制进行调频,本文所提调频控制策略能够使系统频率最快满足国标要求的±0.2Hz 的频率波动范围,系统的频率响应性能最佳。
图 9(b)给出了扰动发生后系统中火电、风电机组出力的变化趋势。由图可以得出,在本文所提调频控制策略下,风电机组能够快速地增发有功输出,补偿了火电机组有功支撑的延时性;此外,结合图 9(a)分析可知,风电机组转速恢复时的额外有功需求降低了系统频率的回复速度,这说明风电机组辅助调频是以延长频率回复时间为代价的。
图 9(c)给出 FIS2 前 40s 的仿真结果。由图可知,在不同频率变化阶段,风电机组模糊惯性控制参数是不断变化的。结合图 9(a)分析,在频率两次下降期间,控制参数 Kdf 和 Kpf的快速增加有效阻尼了系统频率的恶化和加速了系统频率的恢复。此外,输出控制参数曲线具有幅值小且持续时间短的冲击型脉动,分析表明该类脉动是可忽略的。
针对本文所提协调调频控制策略,由于区域Ⅱ 中风电机组所处风速段不同,因此在频率支撑期间每个风速段风电机组的有功出力和转速变化情况也有所不同,具体变化情况如图 10 所示。
对图 10 分析可知,每个风速段的风电机组在频率波动期间均能够提供功率支撑,并且随着风速段等级的提高,风电机组短时有功值逐渐增大,最大为 1.036p.u.;有功支撑(有功出力在 1.0p.u.以上) 时间也逐渐增加,最长为 5.9s,即风电机组短时释放的动能逐渐增多;同时风电机组的转速变化幅度也逐渐增大,最大为 0.003p.u.。
进一步对图 9(a)和图 10(b)进行分析,风电机组转速恢复的同时,系统频率曲线有下凹趋势,但很快又重新恢复,这是因为机组层控制策略以 2Hwmax 作为惯性控制微分系数 Kdf 的最大取值,在提高系统等效惯量的同时又避免了对风电机组的过度依赖,保证了机组的运行稳定;同时可以得出由于不同风速段的风电机组表现出的最大惯量是不同的,因此风电机组是依次进入转速恢复阶段的,在一定程度上削弱了二次频降的强度。——论文作者:盛四清,李朋旺,张立伟,樊茂森
SCISSCIAHCI