发布时间:2022-04-01所属分类:电工职称论文浏览:1次
摘 要: 摘要:为了解决现有光伏电站短期发电量预测方法存在的预测模型复杂、预测误差较大、泛化能力较低的问题,提出一种基于深度信念网络的短期发电量预测方法。首先综合考虑影响光伏出力的环境因素和光伏板的运行参数以及光伏电站历史发电量数据,对深度信念网络进行训练和
摘要:为了解决现有光伏电站短期发电量预测方法存在的预测模型复杂、预测误差较大、泛化能力较低的问题,提出一种基于深度信念网络的短期发电量预测方法。首先综合考虑影响光伏出力的环境因素和光伏板的运行参数以及光伏电站历史发电量数据,对深度信念网络进行训练和学习。在此基础上,采用重构误差的方法确定深度信念网络隐含层层数。最后针对某光伏电站短期发电量进行预测算例分析,验证了该预测模型能主动选择样本抽象特征、自动确定隐含层层数,对短期发电量预测精度较高。对比前馈反向传播(Back Propagation, BP)神经网络预测模型与长短期记忆网络(Long/Short Term Memory, LSTM)预测模型,结果表明所提方法运算量低、预测精度高,且增加神经网络的深度比改进神经网络神经元对预测效果更有效。
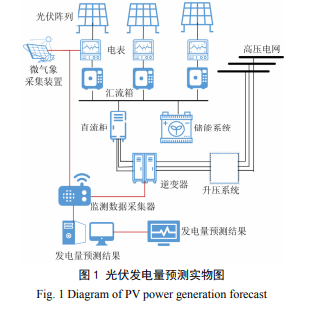
关键词:光伏发电;短期发电量预测;神经网络;深度信念网络;重构误差
0 引言
随着国家大力发展清洁能源相关政策的号召和光伏发电技术的突破,光伏发电站的规模和光伏发电组件的数量不断扩大,光伏发电量占电网总发电量的比例不断增大[1]。针对大规模的光伏电站,巨大数量的光伏板使得其故障排除和定位更加困难,相应更大的电量计量装置和配套通信装置增加了投资成本。通过将光伏电站的预测发电量与实际发电量对比可以实时监测各个光伏阵列的运行状况,若实际发电量与预测发电量存在较大误差,可以快速排除和定位故障所在的光伏阵列区域;同时可以用精度较高的预测模型替代某些光伏阵列的电量计量装置,减少电量计量装置和配套通信装置的投资。因此,精确的光伏电站发电量预测对光伏电站的安全稳定运行和经济运行具有指导意义。
目前,国内外学者对光伏出力预测做了大量相关的研究,提出了自回归和滑动模型(Auto-regressive and Moving Average Forecast Model, ARMA)、灰色理论模型、支持向量机 (Support Vector Machine, SVM)模型、神经网络模型以及组合预测模型等多种预测模型。文献[2]运用 SVM 对输入数据二分类,然后使用 ARMA 模型预测光伏发电出力,但分类器准确度需要进一步提高。文献[3]分析了灰色理论预测算法对光伏出力的预测效果,该方法的局限在于模型预测结果的稳定性受预测日前几天的天气类型相似性影响较大。文献[4]提出了支持向量回归(SVR) 模型的预测方法,采用改进的 KFCM 聚类方法对样本集进行分类处理,并采用多模态 SSO 优化算法对预测模型参数优化,仿真结果表明该方法可用于不同天气的短期光伏发电预测。人工智能算法依据其独特优点也被广泛应用于光伏预测中。文献[5]提出了混沌时间序列改进的 Elman 神经网络对用电量进行预测,采用粗糙集理论修正数据中的峰值点,提高预测精度。文献[6]采用通用回归神经网络和前馈反向传播网络两种神经网络对光伏出力进行预测,结果表明两种方法预测性能良好,后者预测精度更高。文献[7]提出了基于混沌-径向基函数神经网络的光伏预测模型,验证了该模型在不同天气下都具有较好的预测精度。组合优化预测模型的研究焦点在于人工神经网络的优化与改进。文文献[8]提出一种基于改进灰色 BP 神经网络的多模型组合预测方法,将 4 种灰色预测模型的预测结果组合为训练样本,从而训练 BP 神经网络获得其权重系数,降低了求解权系数的难度。文献[9]采用思维进化算法优化的 BP 神经网络、粒子群算法优化的支持向量机和基于单隐层前馈网络极限学习机分别进行光伏发电功率预测,然后使用方差-协方差权值动态分配法组合预测结果,实例证明该方法互补性较强、准确度较高。文献[10]建立了一种基于 LVQ-GA-BP 神经网络测试系统,通过学习矢量量化(Learning Vector Quantization, LVQ)神经网络对样本特征分类,用遗传算法优化 BP 神经网络的参数,算例表明该组合算法比传统算法预测精度更高,BP 神经网络的训练速度更快。文献[11]考虑了气溶胶指数对光伏发电量预测模型的影响,将气溶胶指数作为附加输入参数,通过 BP 神经网络预测下一个 24 h 光伏发电输出,比使用 ANN 的传统方法预测精度更高。
基于以上研究发现,针对短期光伏发电量预测,传统的预测模型较为复杂,预测精度有待提高。神经网络是一种非线性拟合能力较强的网络,可映射光伏发电众多影响因素中的复杂非线性关系,所以可以应用于光伏发电出力的预测。但浅层结构的神经网络,如 BP 神经网络、支持向量机等,由于其网络结构较简单,对样本特征学习不够充分,泛化性受到很大局限,且计算结果容易陷入局部最优解,预测效果精度不高。深度信念网络是包含多隐层的神经网络,通过逐层训练学习的方式主动全面学习样本的抽象特征形成特征空间,弥补传统预测模型和浅层神经网络预测模型的不足,提高预测精度。另外目前的研究主要集中在光伏发电功率的预测以及光伏并网后对电网安全运行的影响,很少有研究光伏发电量的预测及其对电网经济性的影响。本文通过分析光照强度、天气、温度、风速等主要环境因素和光伏电站三相运行参数对光伏电站发电量的影响,建立基于深度信念网络的预测模型,对光伏电站短期发电量进行预测,预测模型和预测结果对实际工程具有实用价值。
1 光伏发电的预测方法和输入变量筛选
1.1 光伏发电的预测方法
光伏发电预测的原理是以天气预报数据或者实测天气数据为基础,结合光伏发电站的地理因素和电站设计参数,建立合适的预测模型并选择合适的算法,从而实现对未来某段时间周期内的光伏发电功率进行预测。根据光伏发电的预测原理,光伏发电预测方法分类有很多,根据预测过程的不同可分为直接预测方法(数据统计法)和间接预测方法(物理法)。
直接预测方法是通过研究大量历史数据的规律,预测未来某时间段内各种天气状况下光伏发电的出力,该方法是以历史数据为基础的,因此也称为数据统计方法。文献[12]基于马尔科夫链对历史数据进行统计和分析,直接预测光伏发电的出力。文献[13]以近 5 年的历史数据为基础,建立了灰色动态模型,对光伏发电出力进行预测。文献[14]根据历史数据采用小波变换和径向基函数神经网络预测次日的光伏发电出力;小波变换法可以有效描述光伏序列的局部特性,神经网络可以表现其非线性特征,因此该组合预测模型预测精度较高。直接预测法必须以历史数据为基础,对预测模型的输入参数要求较高。但是直接预测法可以简化预测过程,减小了预测模型的建模难度。由直接预测方法衍生的人工智能算法也受到广泛的应用。
间接预测方法是通过预测地表或光伏组件接收的光照辐射强度,然后间接预测光伏发电系统的出力。文献[15]采用 Hottel 辐射模型和 Liu-Jordan 辐射模型计算获得太阳辐射强度,从而预测光伏发电系统的出力。文献[16]采用径向基函数神经网络预测地表辐射强度,然后根据光电转换模型最终实现光伏功率超短期预测。文献[17]考虑太阳辐射与风速、湿度和温度等参数之间的相关性,采用小波递归神经网络预测光照辐射强度。文献[18]采用多种人工智能算法预测光照辐射强度,从而计算光伏发电系统出力。间接预测方法先预测光照辐射强度,然后再计算光伏发电系统的出力。这种方法需要进行多次建模和详细的天气预报信息,因此预测过程较为繁琐,结果精度不高。
1.2 预测模型输入变量的筛选
光伏发电系统的发电量由其发电功率和时间决定,光伏发电功率受众多因素的影响,而众多因素又是相互耦合的。
光伏发电出力与光照强度、温度、气象、地理等因素有关。各种因素也是相互影响的,其影响关系如图 2 所示。光伏发电功率的直接决定因素是光照强度,其预测精度直接影响光伏发电功率的预测精度。根据收集得到的数据,研究发现光照强度和光伏出力有明显的对应关系如图 3 所示。由图 3 可知,早上和下午光照强度较低时,光伏输出功率较小,光伏发电量较小;中午光照强度高时,光伏输出功率较大,光伏发电量较大。
温度也是影响光伏发电出力的重要因素,如图 4 所示,光伏出力与温度呈现正相关,温度对光伏发电出力的影响主要表现在太阳能电池性能随温度变化而变化。
气象主要反映某一地区短时间范围内大气的温度和云层情况,其可通过气象仪器测得。其中采集到的数据中也包含光伏电厂的风速和风向等,风速和风向主要通过影响光伏组件的温度分布,从而间接影响光伏发电的出力。选取部分数据绘制光伏发电量和风速的曲线图如图 5 所示,曲线表明风速与发电量之间没有明显的影响关系。下文算例中将进一步研究风速和风向对光伏发电量预测的影响。
地理因素主要反映了光伏发电站的地理位置、地域环境等,其对光伏发电预测的影响比较稳定。本文针对的是某特定光伏电厂,该因素可不予考虑。
本文来源于:《电力系统保护与控制》原刊名《继电器》,创刊于1973年,是由许昌开普电气研究院(原许昌继电器研究所)主办的全国性电工技术类科技期刊,刊期为半月刊,文种为中英文,设有:继电保护、电力系统分析与控制、电网规划设计与可靠性、电力市场、电能质量等栏目。
另外,光电效率、电站设计和人为因素等也会对光伏发电出力造成影响。光电效率主要包括光伏组件和光电站的转化效率,前者指太阳能转化为电能的效率,后者指电能从光伏电站传输到电网的效率。
以上各种影响因素又是相互耦合的。地理因素决定了光伏发电站所处地理位置的气候条件,从而限制了其光资源水平。气候因素不仅影响某时段该地区的气象,也会间接影响光伏组件和光伏电站的光电效率。光电站光伏板的倾角和排列布局也要根据地理位置、气候条件做出相应的设计。
2 光伏发电量的预测模型
通过 1.2 节的分析发现,光伏发电站的出力同时受多个因素的影响,各个影响因素的相互影响关系较为复杂。采用深度信念网络可以映射多因素对发电量的非线性关系,从而应用于光伏电站的短期发电量预测。
2.1 深度信念网络模型
深度信念网络(Deep Belief Network, DBN)是深度学习中的重要模型,是一种概率生成模型,它由一系列的限制玻尔兹曼机(Restricted Boltzmann Machines, RBM)单元组成[19]。RBM 模型每层各个神经单元之间无连接,可视层每个神经单元与隐含层每个神经单元均有连接。DBN 由一系列的 RBM 构成,每层 RBM 的输出作为下一层的输入,其结构如图 6 所示。
DBN 预测模型底层采用多层的 RBM 结构,使用贪婪算法对样本数据进行逐层训练学习,训练第一层 RBM 获得的参数作为第二层 RBM 的输入,依次类推获得每一层的参数,该过程属于无监督学习。
模型顶层使用 BP 神经网络对预测结果进行拟合优化。将底层模型训练学习获得的抽象特征作为顶层 BP 神经网络的输入,通过 BP 神经网络的拟合输出预测结果。同时也需要采用 BP 算法对获得的模型参数进行微调和优化。该过程为有监督学习。
2.2 深度信念网络结构的确定
隐含层神经元的个数和隐含层层数决定了深度信念网络的规模和精度。隐含层神经元数目太多会造成 DBN 规模过大、计算量大、模型训练时间长等问题。而隐含层神经元数目太少会降低预测精度。本文根据文献[20]所提到的 Kolmogorov 定理,当输入变量有 n 个时,隐含层神经元个数一般取 2n+1 个。
深度信念网络对历史数据学习的过程也是对样本特征信息学习和分类的过程。多类样本输入 DBN 后,在逐层训练过程中不同样本间的相关系数会越来越小,并且随着隐含层数目增加,不同样本的特征提取越来越精确,泛化程度提高,样本分类识别的错误概率会越来越小,最终被完全识别。但是,随着隐含层数目增加,模型参数指数增加出现维数灾的问题,增加了模型训练和计算时间,计算效率较低,同时也会出现过拟合的现象。一般确定隐含层层数常采用试验法(穷举法),即依次计算验证列举出来的预测模型,将预测模型获得的预测值与实际值比较,直到达到足够的精度要求。试验法没有一个确定的评估指标判断模型的好坏,主观因素较强,且每次都需要重新训练整个模型,计算方法较为繁琐,计算时间长、效率低,容易出现过拟合现象。针对此问题,本文拟采用文献[21]提出的基于重构误差的判断方法确定 DBN 的深度。
将样本数据通过 DBN 预训练获得的网络计算值与样本数据真实值之间的差值定义为模型的重构误差,如式(9)所示。
采用重构误差可以在训练中自组织地训练深度信念网络,以解决其隐含层层数人为选择的问题,从而有效提高运算效率,降低运算成本。
2.3 样本数据采集与处理
以某光伏发电站为研究对象,利用光伏发电显示器采集光伏发电站光伏板的运行状态参数,包括太阳能电池板背板温度、其组成的光伏阵列的三相电压、电流和功率;利用微气象采集装置采集太阳能辐照度、环境温湿度、风速、风向等气象数据。
通常设备误差或故障以及人为因素等都会造成采集到的光伏历史数据和天气信息数据缺失或异常,因此在使用数据前需要进行补全和修正。平均值法和 K 近邻补全算法是比较常用的数据补全方法。K 近邻补全算法具有有效性高、复杂度相对较低等特点,所以本文采用 K 近邻补全算法对采集到的数据进行补全和修正。根据相邻数据具有很高相似性的特点,选取缺失数据的 k 个最近样本,用它们的平均值补全缺失的数据,其中采用欧氏距离判断样本点之间的距离,如式(11)所示。
2.5 光伏预测流程
在确定深度信念网络的基本网络结构后,需要对所提出的预测模型进行训练学习、验证以及光伏出力预测。基于深度信念网络的预测模型流程图如图 7 所示。
3 算例分析
3.1 DBN 预测模型预测结果分析
本节基于前文所提出的 DBN 预测模型,对某光伏电站部分光伏阵列的发电量进行预测,算例实现基于 Python3.7 平台。本算例中所使用的样本数据均为该光伏发电站部分光伏阵列收集的 9 000 个历史样本。算例中随机选择 8 550 个样本作为 DBN 的训练和测试样本对 DBN 进行训练,选取剩余 450 个样本作为预测样本进行光伏发电量预测,校验预测模型的预测精度。每个样本的数据包括 1 维的光伏发电站历史发电量和 19 维的影响因素变量,具体如表 1 所示。DBN 无监督学习的学习率为 0.000 5,数据批次为 150,训练迭代次数为 200,激活函数为 sigmoid 函数;有监督学习的学习率为 0.005,数据批次为 65,训练迭代次数为 150。为了清晰地展示 DBN 预测模型对光伏发电系统出力的预测效果,绘制发电量实际值与预测值的曲线如图 8 所示。通过图 8 实际值与预测值曲线的对比可以看出,基于 DBN 建立的光伏发电预测模 型预测结果与实际值较为接近,曲线重合度较高。
进一步分析 DBN 预测模型对光伏发电系统发电量预测的误差,采用预测值的相对误差百分数来评估,绘制相对误差百分数的曲线如图 9 所示。
由图 9 可以看出,(1) 基于 DBN 的光伏发电预测模型预测相对误差最大为 0.62%,最小为 0.01%。 (2) DBN 预测相对误差大部分分布在 0.25%以下,只有小部分的预测相对误差大于 0.25%。考虑实际数据采样过程中的误差和截断误差,认为基于 DBN 的光伏发电量预测模型具有较高精确度和有效性。
3.2 数据预处理对预测结果的影响
大量性能良好的历史数据是获得精确深度信念网络预测模型的基础。图 9 为样本数据未经处理的预测结果相对误差百分数曲线。
对比图 9 和图 10 可以明显看出,样本数据未经处理直接作为训练样本会对预测模型的预测精度造成较大影响。这主要是因为未经处理的原始数据可能存在关键数据的缺失、数据异常等情况,这些不完整和异常的数据作为训练样本提取的样本特征不够准确,获得的 DBN 结构中每层隐含层的参数也存在较大误差,直接造成预测模型和预测结果不准确,因此预测结果相对误差呈现图 10 所示情况。另外,对比结果也说明研究中所采用的数据预处理方法,即 K 近邻补全算法对样本数据补全及修正以及拉依达准则剔除异常数据的有效性。
3.3 隐含层层数对预测结果的影响
确定 DBN 的网络结构是建立预测模型的基础,上文提出采用重构误差的方法确定 DBN 的隐含层层数,基于本算例确定 DBN 的隐含层为 2 层。进一步对比当隐含层为 1 层、3 层和 4 层时预测模型的预测结果,如表 2 所示。
对比表 2 可以发现,采用重构误差的方法确定 DBN 预测模型的结构,预测结果最为精确。同时发现当增加隐含层层数多于 2 层时,预测精度反而降低,这是因为增加隐含层后,网络中权值学习迭代次数足够多,拟合了训练数据中无代表性的特征,出现了过拟合现象。
3.4 输入变量对预测结果的影响
为进一步研究各个输入变量对预测结果精度的影响,本节通过删除训练样本中的一些输入变量,对 DBN 预测模型再次进行训练,通过观察预测结果,判断各个输入变量对预测结果的影响程度。实验结果如表 3 所示。
对比表 3 发现,当输入变量中缺少光照强度时,预测结果的平均相对误差变化最大,这说明光照是影响光伏发电量的决定因素;当输入变量中缺少温度时,预测结果的平均相对误差变化结果也较大,这是因为温度是通过影响光伏阵列的转换效率从而直接影响发电量;当缺少风速和风向、转换效率、光伏阵列三相运行参数时,预测结果精度变化不大,这主要是因为这些因素不是影响光伏发电量的直接因素,而是间接影响光伏发电量。
3.5 多种神经网络预测方法预测结果对比
为进一步验证深度信念网络预测模型的精确度和有效性,将其与 BP 神经网络预测模型和长短期记忆网络预测模型的预测结果进行对比。样本数据均采用上文所述数据,三种预测模型的预测结果指标和仿真时间如表 4 所示。
从表 4 可以看出,DBN 预测模型的平均相对误差小于 BP 预测模型和 LSTM 预测模型。同时 DBN 预测模型仿真所需时间较短,表现出良好的运算精度和运算速度。
图 11 和图 12 分别是 BP 预测模型和 LSTM 预测模型预测结果相对误差百分数的曲线图。由图 11 可以看出,基于 BP 神经网络的预测模型预测相对误差最大为 3.5%,相对误差分布在 0.5%以上的样本点较多。主要原因是 BP 神经网络隐含层只有一层,对训练样本的特征学习不准确,泛化性不高,且可能出现了局部最优解。
由图 12 可以看出,基于 LSTM 的预测模型预测相对误差最大为 1.47%,相对误差分布在 0.5%~1% 的较多,且仿真时间最长。对比三种神经网络预测模型的预测误差,可以看出 DBN 神经网络预测模型相比 BP 预测模型和 LSTM 预测模型具有较高的准确性,这说明增加神经网络深度比改进神经网络神经元的预测效果更好。
4 结论
本文针对光伏电站的发电量预测,简单阐述了光伏发电站发电量的预测方法,并详细描述了深度信念网络的基本原理、结构组成和网络深度确定方法、预测模型训练学习、预测的过程,最后建立基于深度信念网络的光伏发电预测模型,并通过算例分析和验证得到如下结论:(1) 算例结果表明该预测模型能够主动有效地学习样本的特征,训练深层架构网络的参数,预测误差大概率分布在 0.5%以下,预测结果较为准确;(2) 所提方法预测结果与 BP 神经网络预测模型和LSTM预测模型预测结果进行对比发现,当样本数据有限时,DBN 预测模型的预测结果平均相对误差小、运算量低、预测精度高;且增加神经网络模型的深度比改进神经网络神经元对预测效果更有效。
本文所采用的 DBN 预测模型对光伏电站的光伏阵列发电量预测精度较高,可应用于光伏发电站的规划建设中,可替代部分光伏阵列电量计量装置,有效降低光伏电站的建设投资成本。同时,也可以实时监测光伏阵列的运行状况,将预测结果与实际发电量对比,在光伏电站出现局部故障情况时,能够指导运行人员快速排除和定位故障光伏阵列所处区域,具有较大的工程价值。但本文所提的预测模型仍具有一定的局限性,每个预测模型只对提供样本的主体有效,不具有普适性,针对大规模的光伏电站其光伏阵列数量较多且相互独立,需要针对性建立预测模型。如何在历史样本有限的情况下进一步提高预测模型的精度,并将基于 DBN 的光伏电站发电量预测方法与工程实践紧密结合,使其更具有普适性,是未来需要重点研究的内容。——论文作者:赵 亮 1 ,刘友波 1 ,余莉娜 2 ,刘俊勇 1
参考文献
[1] FENG Lin, ZHANG Jingning, LI Guojie, et al. Cost reduction of a hybrid energy storage system considering correlation between wind and PV power[J]. Protection and Control of Modern Power Systems, 2016, 1(1): 86-94. DOI: 10.1186/s41601-016-0021-1.
[2] 高阳, 张碧玲, 毛京丽, 等. 基于机器学习的自适应光伏超短期出力预测模型[J]. 电网技术, 2015, 39(2): 307-311. GAO Yang, ZHANG Biling, MAO Jingli, et al. Machine learning-based adaptive very-short-term forecast model for photovoltaic power[J]. Power System Technology, 2015, 39(2): 307-311.
[3] 徐菁. 光伏发电系统短期功率预测方法的研究[D]. 南昌: 南昌大学, 2016. XU Jing. Research on short-term power prediction method of photovoltaic power generation system[D]. Nanchang: Nanchang University, 2016.
[4] 黄予春, 曹成涛, 顾海. 基于 IKFCM 与多模态 SSO 优化 SVR 的光伏发电短期预测[J]. 电力系统保护与控制, 2018, 46(24): 96-103. HUANG Yuchun, CAO Chengtao, GU Hai. Short-term photovoltaic power generation forecasting scheme based on IKFCM and multi-mode social spider optimization SVR[J]. Power System Protection and Control, 2018, 46(24): 96-103.
[5] 吴佳懋, 李艳, 符一健. 基于粗糙集-混沌时间序列 Elman 神经网络的短期用电量预测[J]. 电力系统保护与控制, 2019, 47(3): 23-30. WU Jiamao, LI Yan, FU Yijian. Short-term power consumption prediction based on rough set chaotic time series Elman neural network[J]. Power System Protection and Control, 2019, 47(3): 23-30.
[6] SABERIAN A, HIZAM H, RADZI M A M, et al. Modelling and prediction of photovoltaic power output using artificial neural networks[J]. International Journal of Photoenergy, 2014(6): 1-10.
[7] 王育飞, 付玉超, 孙路, 等. 基于混沌-RBF 神经网络的光伏发电功率超短期预测模型[J]. 电网技术, 2018, 42(4): 1110-1116. WANG Yufei, FU Yuchao, SUN Lu, et al. Ultra-short term prediction model of photovoltaic output power based on chaos-RBF neural network[J]. Power System Technology, 2018, 42(4): 1110-1116.
[8] 王新普, 周想凌, 邢杰, 等. 一种基于改进灰色 BP 神经网络组合的光伏出力预测方法[J]. 电力系统保护与控制, 2016, 44(18): 81-87. WANG Xinpu, ZHOU Xiangling, XING Jie, et al. A prediction method of PV output power based on the combination of improved grey back propagation neural network[J]. Power System Protection and Control, 2016, 44(18): 81-87.
[9] 单英浩, 付青, 耿炫, 等. 基于改进 BP-SVM-ELM 与粒子化 SOM-LSF 的微电网光伏发电组合预测方法[J]. 中国电机工程学报, 2016, 36(12): 3334-3342. SHAN Yinghao, FU Qing, GENG Xuan, et al. Combined forecasting of photovoltaic power generation in microgrid based on the improved BP-SVM-ELM and SOM-LSF with particlization[J]. Proceedings of the CSEE,2016, 36(12): 3334-3342.
[10] 罗建春, 晁勤, 罗洪, 等. 基于 LVQ-GA-BP 神经网络光伏电站出力短期预测[J]. 电力系统保护与控制, 2014, 42(13): 89-94. LUO Jianchun, CHAO Qin, LUO Hong, et al. PV short-term output forecasting based on LVQ-GA-BP neural network[J]. Power System Protection and Control, 2014, 42(13): 89-94.
[11] LIU J, FANG W, ZHANG X, et al. An improved photovoltaic power forecasting model with the assistance of aerosol index data[J]. IEEE Transactions on Sustainable Energy, 2015, 6(2): 434-442.
[12] 丁明, 徐宁舟. 基于马尔可夫链的光伏发电系统输出功率短期预测方法[J]. 电网技术, 2011, 5(1): 152-157. DING Ming, XU Ningzhou. A method to forecast short-term output power of photovoltaic generation system based on Markov Chain[J]. Power System Technology, 2011, 5(1): 152-157.
SCISSCIAHCI