发布时间：2020-08-26所属分类：工程师职称论文浏览：1次
摘 要： 摘 要：根据相似原理，设计了一个坡脚为50的反倾边坡模型、传感器的布置方案和试验的输入方案。为了研究在不同动力反应下反倾边坡的动力响应规律，需要加载不同的地震波以及不同的加速度峰值。试验结果表明： EL Centro波作用下，在反倾边坡坡面和坡内竖直方
摘 要：根据相似原理，设计了一个坡脚为50°的反倾边坡模型、传感器的布置方案和试验的输入方案。为了研究在不同动力反应下反倾边坡的动力响应规律，需要加载不同的地震波以及不同的加速度峰值。试验结果表明： EL Centro波作用下，在反倾边坡坡面和坡内竖直方向上，随着高程的增加，加速度峰值也会增加;通过加速度傅里叶曲线发现，在坡内和坡面上，幅值会随着高程的增加而增加，卓越频率基本位于19.0Hz左右;在EL Centro波的作用下，坡面高程越高，坡内测点和坡面测点的PGA放大系数增大的越快。
关键词 反倾边坡;振动台试验;动力响应规律;PGA放大系数
1 引言
我国国土面积十分辽阔，近年来各地的地质灾害频频发生，加上地形的复杂性，极大地影响着人们的日常生活。在我国的西部地区，特别是山区，滑坡、泥石流等灾害问题是十分突出的，尤其是在地震之后会造成许多的堆积体边坡，从而造成更大的影响[1]。近些年来地质灾害发生的频率显著增加，特别是地震。随着西部大开发战略的持续实施，地震已经成为危害交通线路以及日常生活的一种普遍和危险的地质灾害[2]。如2008年发生在汶川的8.0级强级地震，沿带的四川50多个地区遭受了严重的灾害，造成的经济损失也是巨大的[3];2010年4月14日，青海玉树发生了7.1级大地震，2000多名同胞失去了生命[4]。在地震发生后，可能会诱发大量的岩质滑坡，这些崩滑体既可能阻碍到交通，也可能会形成堰塞湖，极大地威胁到人们生命财产安全。
相关知识推荐：直接向期刊投稿的方法
在实际生活中，地震振动台模拟试验是一种很好的研究方法，能够比较接近实际地震时地震对结构的作用情况，同时也是评价结构物整体抗震能力的一种重要手段。尽管振动台试验在边界条件等方面还存在一定的缺陷，但是就其本身可操作性强等方面的优点，这依然是一种比较实用的研究手段。为了研究反倾边坡的一些特征，本文开展了在模拟地震作用下反倾边坡的动力响应特征，分析反倾边坡在不同荷载下以及坡内和坡面上不同高程的动力响应特征。
2 试验设计及结果分析
2.1 试验设计
本次试验所采用的振动台台面尺寸为3m×3m，最大承重量为10t，最大速度为0.7m/s，工作频率为0.1-50Hz，位移范围为±125mm，最大加速度为15m/s2。鉴于模型以及刚度的要求，本试验采用钢板+型钢制作的刚性模型箱，内空尺寸为2.2m×2 m×1.6m(长×宽×高)，模型的两侧采用的是12mm厚有机玻璃，方便于现场的观察。
为了能够让模型的动力响应比较符合客观实际、比较准确的反映模型原型的动力反应，要让模型与实物之间保持一定的相似性，这对于整个试验最后结果的可参考性是非常重要的。在实际生活中，要做到跟原型一模一样的话需要考虑到资金、台面尺寸等因素，在大多数情况下都会根据相似理论来缩小试验的模型。边坡作为一种半无限体，从理论上来讲是没有边界的，但是在振动台试验之中只能将土体装在有限的容器之内[5]。为了减小边界的影响因素，在模型的两侧放置了泡沫板。
2.2 试验结果分析
在地震的作用下，由于加速度产生的地震惯性力是边坡失稳和变形的主要原因，同时边坡的加速度反应规律是评价边坡动力响应的基本资料[6]。本次试验通过输入不同类型的地震波，并从小到大逐级施加不同振幅的加速度荷载，以此来模拟地震波的作用，目的是为了研究地震频率以及振幅对于在不同高程处的反倾边坡的动力响应规律。
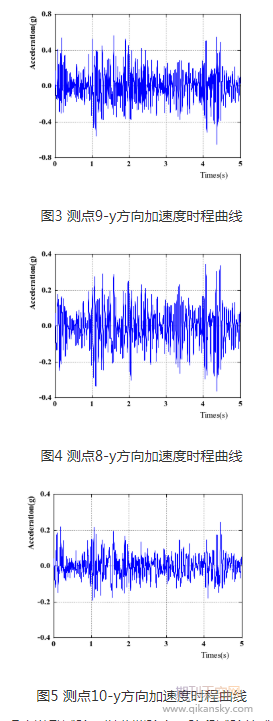
试验加载了不同的波型以及加速度峰值，本文依据的是EL Centro波作为地震激励的试验数据。图3-图5为输入EL Centro波、加速度峰值为0.4g，反倾坡面上的测点9、8、10的y方向上的加速度时程曲线，持时为10s，选取中间段5s作为分析对象。
每一次试验开始之前都会先进行白噪声激励试验，以此消除上一阶段试验的残余影响[7]。从上面的图形可以得到，随着高程的增加，加速度峰值也会增加。
在实际生活中，对工程抗震而言，除其振幅外，还可以通过频谱和持时来进行描述[8]。图7-图9是输入为0.2g的EL Centro波，测点9、8、10的y方向上的加速度傅里叶曲线。
根据试验结果可以发现，反倾边坡在坡面上不同高程的加速度响应具有相似的变化规律，如图6-图8所示，三个测点的卓越频率都在19.0Hz左右。反倾边坡还对傅里叶幅值有着放大的作用，在测点11处，幅值峰值为0.01、测点8处的幅值峰值为0.02、测点9处的幅值峰值为0.03，可见随着高程的增加，幅值也在增大。
图10-图12是在EL Centro波作用下，选取反倾边坡坡内竖直方向上的测点1、3、2的y方向上、输入为0.2g的加速度傅里叶曲线，可以得到：三个测点的卓越频率也都位于19.0Hz左右，在测点1处，幅值峰值为0.022、测点3处的幅值峰值为0.019、测点2处的幅值峰值为0.013，可见随着高程的增加，坡内竖直方向上测点的傅里叶幅值也会被放大，与坡面上的测点的规律是相似的。
在试验之中，地震波的传播特性可以通过加速度放大效应来反映，放大效应常采用加速度峰值的放大系数表示[9]。图14是选取测点6-y方向作为台面测点，用坡面和坡内垂直方向上的测点的峰值加速度除以台面加速度峰值以得到加速度放大系数曲线。
通过图13可以得到，在EL Centro波的作用下，反倾边坡的坡面上所表现出的PGA放大系数变化规律基本是一致的。随着高程的增加，PGA放大系数会被放大，在坡脚处，加速度为0.1g、0.2g、0.4g、0.7g的PGA放大系数分别为0.54、0.35、0.27、0.34;在接近坡面顶部处，加速度为0.1g、0.2g、0.4g、0.7g的PGA放大系数分别为4.33、3.98、3.86、4.79，最大峰值放生在地表处，整个放大过程不是线性的。在放大系数被放大的过程当中，PGA=0.1g、0.2g的增加过程比较顺滑，在0.72m处转折很小，后面的直线斜率变化不大;PGA=0.4g、0.7g曲线在高程到达0.72m处有一个折点，之后的直线斜率变小，放大系数被放大的速度增加，可以得出高程越高，PGA放大系数会被放大的越快，也会越大。在加载EL Centro波的不同加速度峰值的工况下，从图中可以得出关于PGA放大系数的一些规律：在高程0m-0.72m之间，PGA放大系数的大小为PGA=0.1g>0.2 g >0.4 g >0.7 g，在到达接近地面处时，PGA=0.7达到最大值，大小为PGA=0.7g>0.1 g >0.2 g >0.4 g。
图15为在EL Centro波的作用下，反倾边坡坡内竖直方向上的测点的分析结果，从图中可以得到，随着高程的增加，PGA系数也会被放大。在1/3边坡处，也就是高程0.36m处，加速度为0.1g、0.2g、0.4g、0.7g的PGA放大系数分别为1.79、1.66、1.53、1.35;在接近边坡顶部处，加速度为0.1g、0.2g、0.4g、0.7g的PGA放大系数分别为4.33、3.99、3.86、4.8，最大峰值放生在接近地表的测点处。在高程增加到0.36m之前，PGA放大系数都增加的很慢，基本位于1-2之间;在0.72m-0.8m时，PGA的放大速度增快;在0.8m-1.04m之间，PGA放大系数被放大的很快，可见高程越高，PGA放大系数会被放大的越快也越大。在在加载EL Centro波的不同加速度峰值的工况下的规律与坡面上的测点的规律是相似的，在高程0m-0.72m之间，PGA放大系数的大小为PGA=0.1g> PGA=0.2g> PGA=0.4 g > PGA=0.7 g，在到达接近地面的测点时，PGA=0.7达到最大值，大小为PGA=0.7g> PGA=0.1 g > PGA=0.2 g > PGA=0.4 g。
3 结语
本文设计并完成了一组边坡振动台模型试验，通过振动台模型试验，研究了在EL Centro波和Kobe作用下反倾边坡上坡面、坡内垂直方向上不同高程处的动力响应规律，得出了以下结论：
(1)在EL Centro波作用下，随着高程的增加，加速度峰值也会增加。
(2)随着高程的增加，对傅里叶幅值也有放大的作用。在0.2g的EL Centro波作用下，反倾边坡坡面上各个测点的卓越频率都集中在19.0Hz附近，最大幅值发生在测点9，也就是地面;反倾边坡坡内垂直方向上测点的卓越频率也位于19.0Hz左右，随着高程的增加，傅里叶幅值也会增加。无论是在坡面还是坡内，高程增加都会放大傅里叶幅值。
(3)在反倾边坡上，随着高程的增加，各个测点y方向的PGA放大系数被放大，在坡面顶部处达到最大值。在反倾边坡坡面上，在EL Centro波的作用下，PGA放大系数的整个放大过程都比较顺滑;在选取0.4g的工况下，在两个地震波作用下的PGA方大系数曲线是相似的。在反倾边坡坡内垂直方向上，在EL Centro波作用下，高程越高，PGA放大系数被放大的越快。——论文作者：安旭 1，曾海凌 2
SCISSCIAHCI
