0
发表咨询在线!

发布时间:2022-03-07所属分类:工程师职称论文浏览:1614次
摘 要: 摘要:双腔室空气弹簧以其优良的隔振性能及刚度可变特性已经在部分高端车型和赛车上得到使用,但是对其动刚度预报的精确模型及动态特性的深入研究还不够完善。本文基于能量原理从热力学角度出发,结合空气动力学及结构动力学给出了一套双腔室空气弹簧的精确模型并给出

摘要:双腔室空气弹簧以其优良的隔振性能及刚度可变特性已经在部分高端车型和赛车上得到使用,但是对其动刚度预报的精确模型及动态特性的深入研究还不够完善。本文基于能量原理从热力学角度出发,结合空气动力学及结构动力学给出了一套双腔室空气弹簧的精确模型并给出各刚度、阻尼项明确的物理意义。设计示功实验选取了不同振幅和频率的正弦激励对双 /单腔空气弹簧进行实验验证。实验结果表明本文提出的动刚度模型能够很好地反映出双腔室空气弹簧的滞回特性及刚度可变特性,也能够明确反映出动刚度的频率相关性。最后基于模型给出了各参数项对动刚度幅值和滞回相位角的影响规律,基于实验验证了仿真结果并给出规律的物理解释。结果表明,单腔室空气弹簧的动刚度频率特性相位角仅因热交换而存在一个峰值;双腔室空气弹簧的动刚度相位角存在两个峰值,主要是由于热交换(第一峰)与小孔产生的阻尼效应(第二峰)导致。当激励频率趋向于无穷时,由于热交换不充分及腔室之间气体来不及进行交换,故对单/双腔室空气弹簧的动刚度相位角逐渐趋向于零。本文给出的模型预报方法及动态特性可以对单/双腔室空气弹簧的动刚度进行准确估计,并给出了其动刚度的频率相关性及其影响因素及变化规律。本文的结论能够对空气弹簧的整车动力学匹配及设计提供正面的指导。
关键词:汽车工程;滞回特性;热力学;双腔室空气弹簧;动态特性
0 引 言
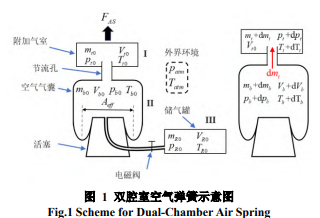
空气弹簧以其优良隔振性能,已经在诸多领域(车辆、航空航天、精密隔振等)[1]得到了普遍应用。在车辆领域,空气弹簧具有轻量化、可调高度、承载能力高、可有效抑制噪声等优点[2]。随着加工技术的进步以及人们对乘坐舒适性的需求日益增高,多腔室空气弹簧应运而生,且已经在多个国外车辆上出现。传统半主动悬架仅包含阻尼可调减振器,不能降低力学传递幅频特性共振峰值;单腔室空气弹簧不能改变刚度,在剧烈工况下不能有效保证平顺性。由此,多腔室空气弹簧将成为未来悬架技术的重要发展方向。所谓多腔室即为空气气囊和附加气室的腔室个数,图 1 展示了乘用车用双腔室膜式空气弹簧(也称带附加气室空气弹簧)系统初始状态及定质量工作过程原理示意图。该系统主要包括承载力的空气气囊、用于调节刚度的带电磁阀的附加气室、充气用的储气罐以及相关管路等零部件。目前针对空气弹簧的建模主要方法有几何学法、等效力学模型、热力学等。
Bruni[3]和 Garcia 等[4]已经对空气弹簧的动力学模型进行详细总结。典型的动力学模型包括在一定频 率 范 围 下适用的 “Nishimura model”,“Simpack model”[5],考虑平方阻尼项的“Vampire model”[6],考虑摩擦单元与速度指数项相关阻尼的“Berg model”[7]等以及一些相应的改进模型[8]。Quaglia 等人[9]分析了该模型的频率特性和阶跃响应并利用线性模型讨论悬架刚度特性。Zhu S.H.等[10]推导出了双腔室的空气弹簧的动态刚度并通过实验进行了理论验证。Li 等[11]基于几何学对铁路用空气弹簧进行垂向刚度建模并进行实验分析和参数讨论。除此之外,该作者还将气体变化过程假设成多变过程并进行仿真分析[12],为后续深入了解空气气囊气体变化过程提供了一定的思路。Liu 等[13]研究了空气弹簧受谐波位移激励的时候动态刚度随腔室之间连接孔面积的变化并进行仿真和实验验证。目前针对空气弹簧的研究大多聚焦于铁路用空气弹簧,对乘用车式双腔室空气弹簧的研究甚少。由于铁路用空气弹簧的附加气室体积较大,且连接管路较长较粗,故有很多学者研究管路、小孔等连接模型并考虑气体振荡现象。Lee[14]、Harris[15]、Zhu[16]等人利用热力学、连接管路模型建立空气弹簧动力学特性并分析气体的振荡过程,为后续热力学建模提供了一定的思路和参考。Facchinetti 等[17]研究了由空气弹簧剪切和侧倾变形之间的准静态耦合效应对车轮/铁路接触力的影响,对行驶安全性和平顺性提升有一定指导意义。Docquire 等[18]基于多体动力学和气体动力学对铁路用空气悬架系统进行建模,并进行了悬架的结构优化。除此之外,Docquire 等[19] 对热交换过程进行敏感性分析并深入研究了双腔室空气弹簧内部的多变过程,研究表明车辆的动力学特性与热交换率有很强的相关性,对后续建模有一定指导意义。Yin 等[20]提出一种新结构空气弹簧并利用气体多变过程推导出动力学模型并与实验进行验证。李芾等[21]对空气弹簧动力学参数进行分析,得出不同参数对空气弹簧动力学特性的影响。陈俊杰等[22]利用线性模型以及试验参数辨识方法对空气弹簧关键设计参数进行标定研究。目前也有学者利用有限元等方法进行空气弹簧的建模和整车匹配工作[23,24]。部分学者利用热力学或实验等方法给出(带附加气室)空气弹簧的等效力学模型,但是少见反映乘用车用双腔室空气弹簧的滞回特性的模型及其影响规律的研究。综上,目前对空气弹簧的研究大部分集中在单腔室或针对铁路用的双腔室囊曲膜式空气弹簧的理论建模,但是这种构造的主要目的是降低刚度但并不可调。除此之外,对空气弹簧动刚度研究主要是基于气体多变或绝热假设进行推导,少见从热力学角度出发推导考虑能量耗散的双腔室空气弹簧的动刚度公式。且对双腔室空气弹簧的滞回特性机理研究不足,未能给出其影响因素和变化规律。
本文拟从热力学和空气弹簧机理模型出发,对乘用车用双腔室空气弹簧的滞回特性和刚度特性进行研究并给出其频响特性和变化规律。本文结构主要分为以下三个方面。首先从能量角度出发,基于热力学、空气动力学、结构动力学推导出双腔室空气弹簧的等效力学模型并给出各项明确的物理意义和精确的数学表达;接着搭建 MTS 实验台架对单/双腔室模型动刚度进行验证;最后依据仿真和实验给出单/双腔室空气弹簧动刚度的频率响应特性以及各项对动刚度的影响规律并给出其物理解释。针对不同车型的动力学匹配可以根据本文的理论新模型及多腔室空气弹簧的动态特性开展。
1 双腔室空气弹簧模型推导
双腔室空气弹簧理论模型推导过程中从能量角度出发,利用热力学第一定律给出气体能量变化规律,再结合空气动力学中的连接孔模型与悬架动力学方程推导出双腔室空气弹簧的动刚度模型。
相关知识推荐:发表论文都是网上投稿吗
本文中假设充放气过程已经结束,整个系统无漏气,为定质量工作系统。首先结合示意图 1 进行基本假设说明:压强为绝对压强;气体质量流量以流入附加气室为正;气体压强 p、温度 T、气体质量 m、体积 V 变化量以变大为正;位移、力 FAS向上为正。对空气取 R 287 J/(kg K) ,比热容比 1.4。下标 t,b,R,0,atm 分别代表附加气室、空气气囊、储气罐、初始状态和外界环境;变化量以 d 表示。
2. 实验描述及分析验证
2.1. 实验描述
本文搭建了 MTS 示功实验平台,并采用某车型用的前轴双腔室空气弹簧设计工装以及实验流程。图 4 展示了 MTS 及空气弹簧实验设备,连接管路采用6 管路连接。利用高压气源将空气弹簧充气,达到工作的力值后通过减压阀进行压强控制。实验数据由 MTS 传感器读取,包括固定采样频率的力传感器值、液压作动器位移、作动器速度、时间等数据。实验前利用打磨工具将减振器中的液压油放出并确定出限位橡胶块的位置,避免减振器对最后结果产生影响。利用排水法多次测试出附加气室的容积。实验中以空气弹簧初始工作状态( 0 0.625m 6825N, 9 bar AS b h F p ,)为初始状态进行实验分析。振幅分别取 A=5;10;15;20;25(mm) 进 行 实 验 ; 在 每 个 行 程 取 激 振 频 率 为 f=0.1;0.5;1;2;5;8;10(Hz)进行实验并记录数据。利用恒压源进行刚度电磁阀开闭的切换,当不给电压时电磁阀开启(双腔室);给定 5V 直流电压时电磁阀关闭(单腔室),在每个行程和频率下分别进行实验。每次实验进行三个周期激励并取中间组为实验值进行数据分析。
2.2. 分析验证
利用搭建的 MTS 台架数据以及仿真模型进行对比分析。为了便于分析和受篇幅所限,本文中给出频率 10Hz 以及振幅 25mm 的单双腔情况下实验和仿真情况,如图 6,图 7 所示。可以看出,前述等效力学模型能够很好地反映空气弹簧的滞回刚度特性,验证了模型的准确性。除此之外,还可以看出单/双腔室的空气弹簧(图 5)中各元件具有一定的频率相关性。下面根据抽象模型的传递特性表达式进行仿真分析各个元件的频率相关性以及对等效动刚度和滞回相角的相关规律。
本文中引入在所有实验激励下最大相对误差作为理论曲线的评价指标。在单腔室情况下最大相对误差为 3.29%;双腔室情况下最大相对误差为 4.21%。结果表明本文提出的理论模型具有较好的拟合效果,可以完整真实地反映出单/双腔室空气弹簧的刚度和滞回特性。
图 8 表示 k1, k2 随变化时动刚度的膜及相位角随频率变化关系。可以看出,对于双腔室空气弹簧来说其动刚度幅值特性呈现出“三阶梯”式的特性。可以粗略将频率范围分为低中高三个频率段,每个频率段对应的刚度呈逐级增加的趋势,且 k1 对高频段的刚度影响较大,对中频段影响较小。这是因为当频率逐渐增大的时候,两个气室之间的气体交换及与外界热交换不充分,附加气室起到的刚度特性逐步减弱且相位角趋向于 0。故在高频段动刚度主要由于空气气囊的刚度决定。同理,k2 主要对中频段的动刚度影响较大,对高频段的影响较小。
图 9 展示了等效阻尼在频域内对动刚度的影响规律。相比较于刚度,等效阻尼的影响主要体现在低中高频段的切换临界频率上。根据图 9(a),单腔室的等效刚度 c1 主要对低到中频段的相位影响较大;连接孔等效刚度 c2主要对中到高频段的相位影响较大。
结合各贡献项对最终动刚度的幅值影响变化关系可知,之所以动刚度幅值特性呈现出向上“阶梯”式特性的物理解释为:随着频率的增加,热交换产生的等效阻尼(单/双腔室空气弹簧)和连接孔产生的等效阻尼(双腔室空气弹簧)均增大。根据动刚度式(13)可知,等效刚度和阻尼项对动刚度的膜值产生正相关影响。从图 9 也可以看出低频峰值主要由热交换产生的阻尼影响;高频峰值主要由小孔产生的阻尼影响。
从上述分析易知单腔室的动刚度幅值呈现“两阶梯”式,相位角仅存在一个峰值。k1 对高频段刚度影响较大;c1 对由低向高转化过程影响较大。利用仿真结果反观实验结果图 6、图 7,可得结论如下:单腔室情况下滞回特性随频率增大呈现出先增大后减小的趋势。由于本实验中最低频率为 0.1Hz,在该频率下仍未见滞回特性呈现减小趋势(在接近准静态情况下滞回特性应当减小),故可以证明确有该峰值存在。在接近此峰值处滞回特性非常明显,通常不能忽略。如图 7(a)中单腔室空气弹簧在 0.1Hz 处的加载-卸载曲线的差值超过 1kN,在实际工程应用中若忽略此滞回特性会导致结果不准确甚至差异较大。双腔室空气弹簧的滞回特性随频率增大存在两个峰值,在达到第二个峰值后滞回特性逐渐减小,这是因为两个腔室之间的气体及热量不能进行充分的交换从而导致由附加气室产生的阻尼特性逐渐减小。
在进行整车悬架动力学匹配时,可以根据需要结合本文给出的解耦结构模型进行不同结构参数的设计。如针对高端车型主要考虑行驶平顺性和舒适性,则可以增大附加气室体积减小中低频激励下的动态响应幅值;针对赛车可以减小节流孔面积,增大阻尼以提升中高频激励下的操纵稳定性等。
3. 结论
提出了考虑气囊和小孔阻尼以及与外界热交换的双腔室动力学模型,给出各参数明确的表达式及物理意义。通过单/双腔室空气弹簧设计实验验证了模型的准确性,并给出各参数变化对动刚度的频率相关性。全文得出的结论如下:
1) 基于热力学、空气动力学、结构动力学给出了双腔室空气弹簧的等效力学模型并将各贡献项解耦表示,给出各项明确的物理意义及数学表达,有助于结合多腔室空气弹簧结构参数进行正向设计;
2) 搭建实验台架验证了模型的准确性,该模型能够很好地反映双腔室空气弹簧的阻尼滞回特性、刚度可调特性;
3) 基于模型和实验给出各刚度阻尼项变化对动刚度影响的频率相关性及其变化规律,给出了变化规律的物理解释。给出了不同车型悬架动力学匹配的理论依据。——论文作者:邬明宇 1,尹航 1,李雪冰 1,张建杰 2,吕靖成 1,危银涛*1
参考文献
[1] SPIROIU M A. Railway Vehicle Pneumatic Rubber Suspension Modelling and Analysis[J]. Material Plastice, 2018, 55(1):24-27.
[2] SHI H L, Guo J, Zhu H, et al. European High-Speed Bogie Technology Review[J]. International Journal of Vehicle Design, 2019, 79(1):43.
[3] BRUNI S, MEIJAARD J P, RILL G, et al. State-of-The-Art and Challenges of Railway and Road Vehicle Dynamics with Multibody Dynamics Approaches[J]. Multibody System Dynamics, 2020, 49(4):1-32.
[4] GARCIA I M, GIL-NEGRETE N, PRADERA-MALLABIABARRENA A, et al. A Survey on the Modelling of Air Springs – Secondary Suspension in Railway Vehicles[J/OL]. [2020-10-28]. DOI: 10.1080/00423114.2020.1838566
[5] PRESTHUS M. Derivation of Air Spring Model Parameters for Train Simulation[D]. Lulea:Lulea University of Technology, 2002.
[6] EICKHOFF B M, EVANS J R, MINNIS A J. A Review of Modelling Methods for Railway Vehicle Suspension Components[J]. Vehicle System Dynamics, 1995, 24(6–7):469–496.
[7] BERG M. A Three-Dimensional Air Spring Model with Friction and Orifice Damping[J]. Vehicle System Dynamics, 1999, 33(Suppl.):528–539.
声明:①文献来自知网、维普、万方等检索数据库,说明本文献已经发表见刊,恭喜作者.②如果您是作者且不想本平台展示文献信息,可联系学术顾问予以删除.

SCISSCIAHCI