发布时间:2022-03-22所属分类:工程师职称论文浏览:1次
摘 要: 摘要: 建立了大型光伏电站的诺顿等效模型,推导了逆变器输出电流和并网点电压表达式,研究了光伏电站中由无功补偿装置、升压变压器漏感、输电线路阻抗等组成的电网阻抗对三相光伏逆变器并联系统谐振现象以及电能质量的影响。 最后建立系统仿真模型进行验证,结果表明
摘要: 建立了大型光伏电站的诺顿等效模型,推导了逆变器输出电流和并网点电压表达式,研究了光伏电站中由无功补偿装置、升压变压器漏感、输电线路阻抗等组成的电网阻抗对三相光伏逆变器并联系统谐振现象以及电能质量的影响。 最后建立系统仿真模型进行验证,结果表明:电网阻抗导致系统存在谐振现象,降低系统电能质量;与输电距离增加相比,光伏电站容量增加更容易导致系统电能质量降低;并网点电压的谐波畸变率远大于逆变器输出电流,并网点电压谐波含量更易超标。
关键词: 光伏; 电站; 逆变器; 电网阻抗; 诺顿等效模型; 谐振; 模型; 电能质量
0 引言
近年来,光伏发电已经受到广泛的关注[1]。 2008 年全世界新增光伏发电装机容量中约有 1 GW 来自 10 MW 及以上容量的光伏电站,我国也计划于甘肃敦煌、昆明石林、青海柴达木盆地等地建设兆瓦级光伏并网电站;随着各国百兆瓦级甚至千兆瓦级光伏电站的建设,光伏电站的大型化和并网化将成为今后发展以及研究的主要方向[2- 3]。
光伏发电系统采用的电力电子逆变器装置的开关频率如果没有躲开产生谐波的范围,则会产生大量的各种频次的谐波;光伏发电系统所配置的用于无功补偿和滤波等作用的并联电容器可能会和线路的电抗发生谐振[4]。 随着并网光伏电站容量的增大,它对电网带来的影响也将增加,特别是对 电网产生的电能质量问题尤其突出[5]。
大容量的并网光伏电站一般建在西部偏远落后地区,并网系统的电网结构比较薄弱[6 - 7]。 此时,变压器漏感和长距离输电线路电抗较大,大型光伏电站连接到长输电线路时,光伏逆变器将产生大量的谐波。 随着并网容量的增大,光伏运行产生的谐波对系统的影响不容忽视[8- 9]。 针对这种情况,光伏电站应在满足电能质量标准前提下,考虑光伏电源渗透率问题[5]。
大型光伏电站接入电网后会给电网安全、稳定和经济运行带来不利影响,同时会影响电能质量[10]。对此,国外已有学者对光伏逆变器并入弱电网中的电能质量问题进行研究。 文献[11 - 12]详细阐释了电网阻抗的参数特性,同时分析了电网阻抗对 PR + HC 控制器低频稳定性的影响。 文献[13]探讨了电网阻抗对逆变器输出电流以及并网点电压的谐波影响。 文献[14]在 2 个并网光伏逆变器并联情况下讨论了无功补偿电容与输电线路阻抗对 LCL 滤波器的谐振影响。 然而,上述研究只针对带 LC 和 LCL 滤波器的单个或者 2 个小容量光伏逆变器,并未涉及带 L 滤波器的大型光伏逆变器并联系统。 L 型滤波器以其结构简单、易于设计的突出优点广泛应用于光伏并网逆变器中。 但目前并未有文献对弱电网中大型光伏并网系统的谐振以及电能质量问题进行深入研究。
本文从大型并网光伏系统的拓扑结构出发,以三相并联逆变器系统为研究对象,通过对各个逆变器进行等效建模,建立了大型并网光伏电站的诺顿等效模型;在考虑无功补偿装置的阻抗、变 压 器 漏感以及输电线路阻抗等电网阻抗条件下,推导了光伏逆变器的输出电流以及并网点电压表达式;采用伯德图详细分析了电网阻抗对系统谐振和电能质量 的 影 响 ;最 后 ,在 MATLAB 环 境 下 进 行 了 仿 真验 证。
1 大型光伏电站等效模型
1.1 大型光伏电站拓扑结构
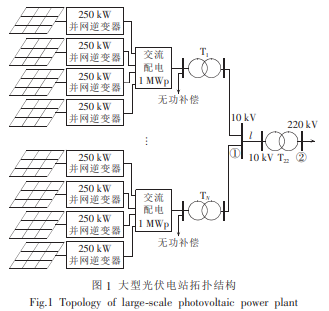
为减少逆变器功率损耗,保证系统的高效性和稳定性,大型光伏电站通常由几组或几十组集中式三相逆变器并联构成。 利用文献[15-16]建立的某大型光伏电站主电路拓扑结构如图 1 所 示。 根据 Q / GDW617—2011《国家电网公司光伏电站接入电网 技术规 定》以 及 GB / T29321—2012《光 伏发电 站无功补偿技术规范》的规定,应在并网关键点(变压器 TN 原 边)配置一定容量的容性无功补偿装置和感性无功补偿装置。 由于容性无功补偿装置的投入会导致并网系统出现谐振现象,因此本文主要研究容 性无功补偿装置对系统 谐振以及电能质量的影响。
图 1 中,250 kW 逆变器输出线电压额定值为 380 V,接入容量为 1.5 MV·A 变压器原边;10 kV 电缆阻抗参数为 0.2 + j0.062 Ω / km。
1.2 电网模型
可控串联补偿器(TCSC)可以平滑而迅速地改变输电线路的阻抗,具有改善网络潮流分布、提 高输送功率、降低短路电流、提高暂态稳定极限、改善系统动态性能、抑制次同步谐振等功能,这些 都 为远距离交流输电提供了很好的技术手段[17]。 因此将 220 kV 及以上超高压长距离输电网络及其电网等效为理想电压源。 建立电网等效模型如图 2 所示,图中参数均折算到逆变器输出电压等级。
图 中 ,Rg 为 10 kV 输电线路等效电阻 ;Lg 为 10 kV 输电线路和变压器 T22 等效电感 之 和;LTN 为升 压 变压 器 TN 等 效电感;CQN、LQN、RQN 分 别为第 N 个 MW 级模块投入无功补偿装置总等效电容、等效电感和等效电阻;upccNk(k = a,b,c)为第 N 个 MW 级模块逆变器并网点电压;ugk(k = a,b,c)为电网电压。
1.3 单个逆变器等效模型
第 i 个 MW 级模块中第 j( j = 1,2,3,4)个三相逆变器在两相静止坐标系下的瞬时功率控制策略如 图 3 所 示 [18],图 中 Gcij(s)为 电流控制器传递函数,采用准 PR 控制器实现两相静止坐标系下无静差跟踪[18],Gcij(s) = kpij + 2krijs / (s2+ 2ωc s +ω2 0)。 系统参数为:电网频率 fg= 50 Hz,直流链电压 U* dcij=600 V,开关频率 fsij= 5 kHz,滤波器电感 Lij=79.1 μH,无功补偿电容 CQi= 0.33 mF,无功补偿电感 LQi= 1.32 μH,无功补偿电阻 RQi = 0.017 Ω。
大型光伏电站中每组并网逆变器系统通常采用相同的结构、参数和控制策略等且升压变压器的型号相同,因此假设图 1 中所有逆变器和变压器的参数完全相同。 从图 1 和图 3 中可以看出:在单个 MW 级模块中,第 1 个 MW 级模块中第 1 个逆变器的输出电流经过由逆变器滤波电感 L11(相当于滤波电感 1),容性无功补偿装置的等效阻抗 CQ1、LQ1 和 RQ1 (相当于 C)以及升压变压器电感 LT1、输 电线路 阻抗 Lg、Rg(相当于滤波电感 2)构成的等效 LCL 滤波器;此时,系统存在 1 个谐振峰。 对于多个(2 个及以上)MW 级模块并联系统,逆变器输出电流经过 2 条路径形成回路。 除了单个 MW 级模块中存在的路径外还增加了第 2 条路径,即第 1 个 MW 级模块中第 1 个逆变器的输出电流经过滤波电感 L11、升压变压器电感 LT1 和第 i(i = 2,3,…,N)个 MW 级模块的升压变压器电感 LTi(这 N-1 个 LTi 并联)(由 L11、LT1 和 LTi 构 成滤波 电 感 1),第 i(i = 2,3,…,N)个 MW 级模块容性无功补偿装置的等效阻抗 CQi、LQi、RQi(这 N-1 个无功补偿装置的等效阻抗并联构成 C),第 i (i = 2,3,…,N)个 MW 级模块的滤波电感 L2ij( j = 1,2,3,4)(这 4N-4 个 滤波电 感 L2ij 并 联构成 滤 波电 感 2)形 成回路,由 此 构 成 了 第 2 个 等效的 LCL 滤波器。 因此,多个 MW 级模块并联时,谐 振 峰 数量 增 加 了 1 个,系 统只存 在 2 个 谐振峰。
将文献[19]所提出的诺顿等效模型的建模方法拓展到三相并联逆变器系统中,建立开环情况下第 i 个 MW 级模块中第 j 个三相逆变器诺顿等效模型如图 4 所示。
1.4 大型光伏电站诺顿等效模型
将上述建模方法应用于所有并联逆变器中,可得 a 相逆变器的诺顿等效模型如图 5 所示。
2 光伏电站电能质量分析
光伏电站中 L 滤波器与无功补偿装置阻抗、升压变压器漏感以及输电线路阻抗等构成的电网阻抗相互耦合使得逆变器输出电流畸变,导致光伏逆变器并网点电压谐波含量超标,威胁着光伏电站并网电能质量。 由于大型光伏电站中每组并网逆变器系统通常采用相同的结构、参数和控制策略等,因此在相同的参数及工作条件下,本文采用伯德图分别研究大型光伏电站容量和输电距离变化情况下系统的谐振机理及电能质量。
随着光伏电站 MW 级模块数 N(对应光伏电站容量为 N MW)增加,开环传递函数 Grij(s)与 Gpcci(s)的对数频率特性曲线如图 6(a)、(b)所示。 当光伏电站输电距离 l 增大(10 kV 输电线路的输电距离一般不超过 10 km)时,开环传递函数 Grij(s)与 Gpcci(s)的对数频率特性曲线如图 6(c)、(d)所示。
理想情况下带 L 滤波器的并网光伏逆变器系统不存在谐振现象,但在实际系统中由于无功补偿装置阻抗、升压变压器漏感以及输电线路阻抗的影响,造成逆变器输出电流和并网点电压传递函数中出现新的反谐振峰和谐振峰,易造成系统出现不稳定现象。 由图 6 可知,当 1 个 MW 级光伏模块并网时,系统存在 1 个反谐振峰和谐振峰,其 谐振频 率为 1 . 71 kHz ; 当 2 个 MW 级光伏模块并联时 ,传递 函数出 现 2 个反谐振峰和谐振峰,谐 振频率 为 1.68 kHz 和 1.75 kHz;当 4 个 MW 级光伏模块并联时,传递函数也包含 2 个反谐振峰和谐振峰,谐 振频率为 1.62 kHz 和 1.75 kHz。 可以看出:当多组(2 组及其以上)MW 级模块并联时系统包含 2 个谐振峰。 输电距离由 5 km 增加为 10 km 时,系统谐振频率由 1.71 kHz 减小为 1.68 kHz。
由图 6 可知,逆变器并联模块数 N 对逆变器输出 电 流 传 递 函 数 Grij (s) 和并网点电压传递函数 Gpcci(s)开环增益影响较小。 但是大型光伏电站容量由 1 MW 增加为 N MW(N ≥ 2)时,系统包含 2 个谐振峰,谐振频率处谐波含量增大,导致逆变 器 输 出电流以及并网点电压谐波含量增加,电能质量降低。同时,光伏电站输电距离 l 的增大使得并网点电压传递函数 Gpcci(s)开环增益增大,并网点电压对谐波的抑制能力减弱,并网点电压谐波含量升高。
3 仿真验证
为验证理论分析的正确性,根据图 3 三相光伏并网逆变器控制原理和系统参数 ,在 MATLAB / Simulink 中搭建了如图 1 所示的大型并网光伏电站系统模型。 考虑到仿真的精度和系统的复杂度,以 3 MW 光伏并网系统为例验证理论分析的正确性。考虑到不同光伏电站通常具有不同的容量和输电距离,因此针对不同的光伏电站容量以及输电距离验证本文理论分析的正确性。
输电距 离 为 5 km 情 况下,大型光伏电站容量分别为 1 MW、2 MW 以及 3 MW 时,第 1 个 MW 级光伏模块中第 1 个逆变器的输出电流波形以及第 1 个 MW 级光伏模块的并网点电压波形分别如图 7 (a)、 (b)和 (c)所 示 ,对 应 的 FFT 分 析 如 图 7 (d)、(e)和(f)所示。 每个子图中的上图对应逆变器输出电流,下图对应并点电压。
从 图 7 可 以看出,光伏电站容量为 1 MW 时,系统谐振频率为 1.69 kHz;当光伏电站容量增加到 2 MW 时,系统谐振频率为 1.65 kHz 和 1.75 kHz;当光 伏电站 容 量 增 加 到 3 MW 时,系统谐振频率为 1.59 kHz 和 1.75 kHz。 当光伏电站容量增加时,逆变器输出电流基波幅值由 531.9 A 分别减小到 531.8 A 和 524.7 A,谐波畸变率由 0.45% 分别增加到 0.48% 和 0.53 %;并网点电压基波幅值由 310.7 V 分别增大到 310.9 V 和 311.1 V,谐波畸变率由 1.46 % 分别增大到 1.74% 和 2.31%。 可以看出:当多组(2 组及其以上)MW 级模块并联时系统包含 2 个 谐振峰,并且随着并网光伏电站容量的增加,逆变器输出电流和并网点电压谐波畸变率增大。
相关知识推荐:光伏电站相关最新发表的论文
电网阻抗对并网点电压电能质量的影响远大于逆变器输出电流,并网点电压谐波畸变率大于逆变器输出电流。 根据 Q / GDW617—2011《国家电网公司光伏电站接入电网技术规定》规定并网点电压谐波畸变率应不超过 5%;对于大容量光伏电站,应在光伏电站出口处加装滤波装置滤除光伏电站产生的大量谐波。
光伏电站容量为 1 MW 时,光伏电站输电距离为 10 km 情况下,第 1 个 MW 级光伏模块中第 1 个逆变器的输出电流波形以及第 1 个 MW 级光伏模块的并网点电压波形如图 8(a)所 示;对 应的 FFT 分析如图 8(b)所示。
对比图 7(a)和 8(a)可知:当光伏电站输电距离由 5 km 增至 10 km 时,系统谐振频率由 1.69 kHz 减至 1.62 kHz。 随着光伏电站输电距离增加,系统谐振频率减小。 当光伏电站输电距离增加时,基波幅值为 531.9 A 基本不变,谐波畸变率由 0.45 % 增 至 0.49%;并网点电压基波幅值为 310.7 V 基本不变,谐波畸变率由 1.46% 增至 1.87%。 随着输电距离增加,逆变器输出电流和并网点电压基波幅值基本不变,但逆变器输出电流和并网点电压谐波含量增大。
4 结论
本文分析了电网阻抗对大型并网光伏系统的谐振以及电能质量的影响,建立了大型并网光伏系统的诺顿等效模型,推导了光伏逆变器输出电流以及并网点电压的表达式,并且通过伯德图和仿真分析研究了由容性无功补偿装置、升压变压器漏感以及输电线路阻抗等组成的电网阻抗对系统谐振以及电能质量的影响,得出的结论如下。
a. 假设所有逆变器和变压器的参数完全相同情况下,大型光伏电站中由于容性无功补偿装置的存在,对于单组 MW 级模块而言,相当于使得光伏逆变器中的 L 滤波器等效为 LCL 滤波器,系统存在 1 个谐振峰。 大型光伏电站中存在多组 MW 级模块并联时系统包含 2 个谐振峰,导致逆变器输出电流以及并网点电压存在大量高次谐波,系统并网电能质量严重降低。
b. 当光伏电站容量增加时,电网阻抗的耦合作用导致逆变器输出电流以及并网点电压谐波含量增加。 并网点电压谐波畸变率远大于逆变器输出电流,并网点电压谐波含量更易超标。 因此,大型光伏电站出口处应加装滤波装置滤除光伏电站的谐波。
c. 与光伏电站输电距离增加相比,大型光伏电站容量的增加更容易导致并网光伏系统电能质量降低。 对于大容量光伏电站,由电网阻抗导致的系统谐振和谐波更加严重,甚至不满足并网要求。
本文的研究结果为大型光伏电站接入弱电网中谐波机理及其抑制方法的研究提供了一定参考,对今后大型光伏电站的建设具有一定的指导意义。——论文作者:周 林,张 密
参考文献:
[1] 李斌,袁越. 光伏并网发电对保护及重合闸的影响与对策[J]. 电力自动化设备,2013,33(4):12-17. LI Bin,YUAN Yue. Impact of grid-connected photovoltaic power generation on protection and reclose,and its countermeasures [J]. Electric Power Automation Equipment,2013,33(4):12-17.
[2] 陈炜,艾欣,吴涛,等. 光伏并网发电系统对电网的影响研究综述[J]. 电力自动化设备,2013,33(2):26-32,39. CHEN Wei,AI Xin,WU Tao,et al. Influence of grid-connected photovoltaic system on power network[J]. Electric Power Automation Equipment,2013,33(2):26-32,39.
[3] 杨秀媛,刘小河,张芳,等. 大型太阳能并网发电模型及应用[J]. 中国电机工程学报,2011,31(增刊 1):19-21. YANG Xiuyuan,LIU Xiaohe,ZHANG Fang,et al. Model of large PV and its applications on power system analysis[J]. Proceedings of the CSEE,2011,31(Supplement 1):19-21.
[4] 康潇. 风电并网对系统稳定.性的影响及改善措施研究[D]. 保定:华北电力大学,2011. KANG Xiao. Research on the effect of grid-connected wind farms on power system stability and improvement measures [D]. Baoding:North China Electric Power University,2011.
[5] 沈文涛. 光伏发电并网系统的电能质量问题研究[D]. 保定:华北电力大学,2012. SHEN Wentao. Research on power quality problem of gridconnected photovoltaic generation system[D]. Baoding:North China Electric Power University,2012.
[6] 周任军,黄灵资,王靓,等. 基于风险和条件风险方法的光伏电站并网极限容量计算[J]. 电力自动化设备,2012,32(6):1-4. ZHOU Renjun,HUANG Lingzi,WANG Liang,et al. Capacity limit calculation based on ri sk and conditional risk method for gridconnected photovoltaic power station[J]. Electric Power AutomationEquipment,2012,32(6):1-4.
SCISSCIAHCI