发布时间:2018-07-18所属分类:科技论文浏览:1次
摘 要: 摘要 本文考虑一类具有强迫力的摆型碰撞振子无穷多次调和的弹性周期解的存在性. 通过坐标变换的方法把碰撞系统转化为定义在全平面上的等价系统, 再运用相平面分析的方法对变换后系统的解的动力行为进行分析, 通过在改进的 Poincare 映射上应用 Poincare-Birk
摘要 本文考虑一类具有强迫力的摆型碰撞振子无穷多次调和的弹性周期解的存在性. 通过坐标变换的方法把碰撞系统转化为定义在全平面上的等价系统, 再运用相平面分析的方法对变换后系统的解的动力行为进行分析, 通过在改进的 Poincar´e 映射上应用 Poincar´e-Birkhoff 扭转定理得到了无穷多次调和的弹性周期解的存在性.
关键词 摆型碰撞振子 弹性周期解 Poincar´e 映射 Poincar´e-Birkhoff 扭转定理
1 引言
本文考虑具有强迫力的摆型碰撞振子
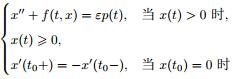
的无穷多次调和的弹性周期解的存在性问题, 其中 ε 是小参数; p(t) 是连续的 2π 周期函数; f(t, x) 是连续函数, 关于 t 和 x 都是 2π 周期的, 并存在正常数 α 和 β, 满足
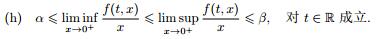
碰撞振子是非线性振动和非光滑 Hamilton 系统的重要模型, 它的行为与 Fermi 加速器问题[1]、对偶弹球问题[2, 3] 和天体力学问题[4] 等相关联, 所以, 研究它具有广泛的实际意义. 同时也为检验一些非光滑动力系统的数学方法提供了一个很好的模型. 但由于系统的非光滑性导致研究的数学工具比较缺乏, 而且碰撞问题的弹性解的全体并不封闭, 从而也缺乏适当的泛函框架, 使得解决碰撞系统的相关问题变得困难.
为了更好地叙述问题, 我们先给出在 x = 0 处发生完全碰撞的弹性解的定义.
定义 1.1 连续函数 x : R → R 称为方程 (1.1) 的碰撞弹性解, 若以下条件成立:

周期弹性解是碰撞振子特有的非平凡的平衡态. 关于碰撞振子的周期解理论的研究方法主要有两类, 一类是应用非光滑临界点理论来研究. 早在 20 世纪 80 年代, Chang [5, 6] 就发展了非光滑临界点理论对障碍问题进行研究. 近期的进展可参见文献 [7] 等. 碰撞振子是一类特殊的障碍问题. Jiang [8] 克服了一些技术上的难点, 通过一些转换, 用非光滑临界点理论, 证明了在超线性条件下, 无穷多弹性周期解的存在性.
另一类是通过适当的作用 - 角变量的选择来克服非光滑性, 把问题转化为适当的相平面上的保面积同胚进行研究. 这样可以应用保面积同胚的一些重要定理, 例如, Poincar´e-Birkhoff 扭转定理得到碰撞振子的无穷多个弹性周期解的存在性 (参见文献 [1,9–11]). Bonheure 和 Fabry [9] 利用 Poincar´e 映射和逼近的方法证明了带有常系数的线性碰撞振子的 2π 周期弹性解的存在性. 接着, Qian 和 Torres[10, 11]用后继映射直接分析碰撞振子的行为, 对更广泛的模型得到了比文献 [9] 更丰富的结果.
对于本文考虑的具有强迫力的摆型碰撞振子, 一个典型的例子就是弹性数学摆
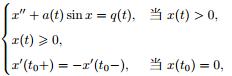
其中 a(t) 和 q(t) 是 2π 周期函数, a(t) > 0. 当 a(t) = 1 和 q(t) = 0 时, 由对称性可知, 其相图就是摆型方程 x'' + sin x = 0 对应于 x大于等于0 的部分. 如果 a(t) 不是常值函数, 或者具有强迫力 q(t), 则 (1.2) 在相平面上的表现就不那么规则了.

的非退化条件或者对 q(t) 有一定的限制条件下, 近期也有一些无穷多个次调和解存在性的结果[15–17]摆型碰撞振子 (1.2) 的弹性周期解的研究尚未见系统的理论结果. 所以, 一个自然的问题是, 在什么条件下摆型碰撞振子 (1.2) 存在无穷多个次调和的弹性周期解. 由于从 (1.2) 的特例的相图 (如q(t) ≡ 0) 可见, 初速度比较大的解其后继映射是没有定义的, 所以, 我们并不能沿用文献 [1, 9–11] 的方法, 必须考虑不同的相平面. 为此, 我们引入文献 [18] 中的坐标变换把碰撞系统转化为定义在全平面上的等价系统, 再运用相平面分析的方法对变换后系统的解的动力行为进行分析, 通过新系统的Poincar´e 映射的性质来研究具有强迫力的摆型碰撞振子的弹性周期解的存在性.
下面是我们的主要结论.
定理 1.1 设 f(t, x) 关于 t 和 x 是 2π 周期的连续函数, 满足条件 (h), p(t) 是连续的 2π 周期函数, 则存在 ε0 > 0, 使得当 |ε| 小于等于 ε0 时, 有 mε ∈ N; 对 m > mε, m ∈ N, 碰撞振子 (1.1) 至少有两个 2mπ周期的弹性次调和解。
2 坐标变换
由于碰撞振子的解要满足 x(t) > 0, 所以其对应的相平面只是右半平面. 在这样的相平面上, 经典的研究平面 Hamilton 系统周期解存在性的 Poincar´e-Birkhoff 扭转定理无法应用. 因此, 我们引入一个新的极坐标变换, 使得在新坐标下碰撞振子的相平面是全平面. 其几何直观是将负半 y 轴拉到正半 y轴使它们重合 (对应弹性碰撞). 因此, 碰撞振子的相平面就是全平面了. 在这种坐标下, 方程 (1.1) 的次调和的弹性周期解对应为 Poincar´e 映射的周期不动点. 下面介绍所用的极坐标变换.

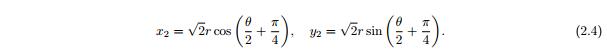


使得 r(t) 和 θ(t) 在碰撞时刻 t0 处是连续函数. 当情形 2 发生时, 取 j = 2k − 1, 我们可以通过类似的方法补充 r(t) 和 θ(t) 在 t0 时刻的定义使其是连续函数.通过在每个碰撞时刻补充定义, 方程 (2.5) 的解 r(t) 和 θ(t) 在其最大存在区间上是连续函数. 容易看出, θ′(t0) = −2 < 0, 因此振子不会在 θ(t) = 2kπ + π/2 (k ∈ Z) 处停留, 并且碰撞前后解满足的方程在情形 1 与 2 之间相互交替. 反过来, 如果方程 (2.4) 的解存在时刻 t˜ 满足 θ(t˜) = 2kπ + π/2, 显然,
方程 (2.1) 对应的解将在 t = t˜ 时发生碰撞.当 θ ∈ (−3π/2, π/2) 时, 有 θ + 2π ∈ (π/2, 5π/2), 由此容易验证, 在方程 (2.2) 中, x(r, θ) 和 y(r, θ)关于 θ 是 2π 周期的.
如果 Hamilton 系统
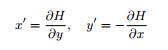
满足解对初值的存在唯一性, 那么除去原点外, 方程 (2.2) 也满足解对初值的存在唯一性. 如果解都是全局存在的, 则容易证明其 Poincar´e 映射
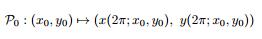
是有定义的, 而且是保面积同胚. 故由极坐标
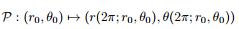
表示的 (u = r cos θ, v = r sin θ) 相平面的 Poincar´e 映射也是有定义的, 在变换 (2.3) 和 (2.4) 的极坐标下, 原来的 (x, y) 相平面有面积元 rdrdθ. 而在变换后的 (u = r cos θ, v = r sin θ) 相平面也有面积元rdrdθ, 而且其 Poincar´e 映射也是保面积同胚.
3 相平面分析
由于我们是在一个特定的环域内应用 Poincar´e-Birkhoff 扭转定理, 因此, 我们的相平面分析可以归结在一个紧区域内, 所以, 不妨假设在定理 1.1 的条件下, 二阶 Hamilton 方程 x′′ + f(t, x) = εp(t) 和Hamilton 系统
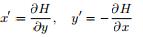
的初值问题的解是存在唯一的, 否则可以像文献 [19] 那样先考虑解析的方程, 然后用一点紧性讨论, 逼近到原方程问题的解.
下面的引理说明我们可以通过极坐标系统 (2.5) 来研究碰撞振子 (2.2) 的次调和解.






4 定理 1.1 的证明
考虑的 Poincar´e 映射在原点处是例外的, 所以, 我们需要用到一个 Poincar´e-Birkhoff 扭转定理的
新的形式 (参见文献 [11, 定理 2.1]), 它是在 Ding [20] 和 Franks[14] 得到的 Poincar´e-Birkhoff 扭转定理的基础上改进的. 这个形式的特点是, 只需要 Poincar´e 映射在某一个包含原点的圆盘外有定义.

它们对应到碰撞系统 (2.2) 的 2 个 2mπ 弹性周期解, 并且分别在 2mπ 时段内恰好有一次碰撞. 所以,它们必定是 2mπ 弹性次调和的周期解. 对每一个 m, 取不同的 r+ 可以构造不同的环域, 得到系统对每个 m > m0 有至少 2 个 2mπ 弹性次调和的周期解.
下面需证明这些周期解是系统 (2.1) 的. 也就是证明这些周期解位于圆盘 r 6 ρ1 之外. 为此, 注意到由 Poincar´e-Birkhoff 扭转定理得到的周期解从 A 中出发, 如果其达到圆盘 r 6 ρ1 必定在某个时刻 t1与内边界 r = r− 相交, 然后又在 t2 时刻与 r = ρ1 相交. 引理 3.3 实际上证明了从内边界 r = r− 出发的解到达 r = ρ1 至少需要用 12π/α 长的时间, 故 2mπ > t2 > t1 + 12π/α. 而引理 3.3 实际上也证明了在 12π/α 时段内解至少顺时针转了 3 圈. 于是, 结合 (3.3) 可得
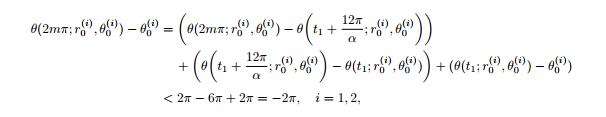
与 (4.1) 矛盾.
我们证明了所得的 2mπ 弹性次调和的周期解是系统 (2.1) 的, 也即证明了对每个 m > m0, 碰撞振子 (1.1) 至少有两个 2mπ 弹性次调和的周期解.
参考文献
1 Lamba H. Chaotic, regular and unbounded behaviour in the elastic impact oscillator. Phys D, 1995, 82: 117–135
2 Boyland P. Dual billiards, twist maps and impact oscillators. Nonlinearity, 1996, 9: 1411–1438
3 Zharnitsky V. Invariant tori in Hamiltonian systems with impacts. Comm Math Phys, 2000, 211: 289–302
4 Corbera M, Llibre J. Periodic orbits of a collinear restricted three body problem. Celestial Mech Dynam Astronom, 2003, 86: 163–183
5 Chang K C. The obstacle problem and partial differential equations with discontinuous nonlinearities. Comm Pure Appl Math, 1980, 33: 117–146
6 Chang K C. Variational methods for non-differentiable functionals and their applications to partial equations. J Math Anal Appl, 1981, 80: 102–129
7 Jiang Q, Tang C L. Periodic and subharmonic solutions of a class of subquadratic second-order Hamiltonian systems.J Math Anal Appl, 2007, 328: 380–389
8 Jiang M Y. Periodic solutions of second order differential equations with an obstacle. Nonlinearity, 2006, 19: 1165–1183
9 Bonheure D, Fabry C. Periodic motions in impact oscillators with perfectly elastic bounces. Nonlinearity, 2002, 15:1281–1297
10 Qian D, Torres P J. Bouncing solutions of an equation with attractive singularity. Proc Roy Soc Edinburgh Sect A,2004, 134: 210–213
11 Qian D, Torres P J. Periodic motions of linear impact oscillators via the successor map. SIAM J Math Anal, 2005, 36:1707–1725
12 You J. Invariant tori and Lagrange stability of pendulum-type equations. J Differential Equations, 1990, 85: 54–65
13 Mawhin J, Willem M. Multiple solutions of the periodic boundary value problem for some forced pendulum-type equations. J Differential Equations, 1984, 52: 264–287
14 Franks J. Generalizations of the Poincar´e-Birkhoff theorem. Ann of Math (2), 1988, 128: 139–151
15 Fonda A, Willem M. Subharmonic oscillations of forced pendulum-type equations. J Differential Equations, 1989, 81:215–220
16 Martinez-Amores P, Mawhin J, Ortega R, et al. Generic results for the existence of nondegenerate periodic solutions
of some differential systems with periodic nonlinearities. J Differential Equations, 1991, 91: 138–148
17 Boscaggin A, Ortega R, Zanolin F. Subharmonic solutions of the forced pendulum equation: A symplectic approach.Arch Math, 2014, 102: 459–468
18 孙西滢. 弹性碰撞振子的动态行为. 硕士学位论文. 苏州: 苏州大学, 2003
19 Ding T, Zanolin F. Periodic solutions of Duffing’s equations with superquadratic potential. J Differential Equations,1992, 97: 328–378
20 Ding W. A generalization of the Poincar´e-Birkhoff theorem. Proc Amer Math Soc, 1983, 88: 341–346
SCISSCIAHCI