发布时间：2022-03-28所属分类：农业论文浏览：1次
摘 要： 摘 要: 通过对前人的试验成果进行整理，得到冻土动力学参数随温度、频率、应变幅、含水量和围压等因素的整体变化规律. 整体上看，冻土的动弹性模量和动剪切模量随温度的降低而增大、随荷载振动频率的增加而增大、随动应变幅的增加而减
摘 要: 通过对前人的试验成果进行整理，得到冻土动力学参数随温度、频率、应变幅、含水量和围压等因素的整体变化规律. 整体上看，冻土的动弹性模量和动剪切模量随温度的降低而增大、随荷载振动频率的增加而增大、随动应变幅的增加而减小、随含水量的增加先增大后减小、随围压的增加而增大; 冻土的泊松比随温度的降低而增大; 冻土的阻尼比随温度的降低而减小，随频率、应变幅、含水量、围压的变化规律性不强. 通过对试验条件和数值模拟时的实际工况对比分析，给出如下建议: 动弹性模量和动剪切模量的预估适合用两段式线性模型，- 5 ℃ 可以作为两段式的分界点; 列车荷载作用下冻土的动力响应属于小应变幅的振动，冻土动力学参数应选择波速法的试验结果.
关键词: 冻土; 动模量; 阻尼比; 泊松比; 动三轴法; 波速法; 温度
0 引言
随着人类活动空间的扩展和对资源需求的增加，寒区的工程建设逐渐增多. 譬如，我国已在寒区进行了青藏公路、青藏铁路、格 - 拉输油管线、中俄输油管线等工程的建设，而冻土独特的物理、热学和力学性质以及动力荷载的复杂性使得在寒区进行工程建设时必须综合考虑冻土和动力荷载问题[1 - 4]. 寒区工程建设时的机器振动、列车和高速汽车的车辆振动、地震作用等都会对寒区道路路基和构筑物基础施加动荷载，因此冻土的动力学特性研究对于寒区工程建设具有重要意义. 进行寒区工程抗振设计时，需要进行各种计算，而计算结果能否较好地反映实际情况并较好地预测可能发生的情况，关键在于选择合适的计算模型以及冻土动力学参数. 有学者认为冻土动力学的计算模型可以采用未冻土的[5 - 9]，事实上目前也没有专门针对冻土的动力学计算模型，然而，应注意冻土的动力学参数与未冻土有较大差异. 国内外学者对冻土动力学参数进行了大量的研究，本文通过整理国内学者的研究成果，分析总结冻土动力学参数的变化规律，供寒区工程设计和计算时参考.
1 冻土动力学参数试验和计算方法
冻土动力学参数的室内测定方法主要有超声波法、共振柱法和动三轴 法. 超声波法适用于 10 - 7% ～ 10 - 5% 范围内的小变形; 共振柱法适用于 10 - 6% ～ 10 - 3% 范围内的小至中等变形; 动三轴法适用于 10 - 3% ～ 10 - 1% 范围内的中等到大变形[10].国内学者对冻土动力学参数的研究主要采用超声波法和动三轴法.
2 冻土动力学参数的国内研究成果
国外在 20 世纪 60 年代就开始研究动荷载作用下冻土的动力响应特征，尤其是冻土动力学参数的变化特征. 我国从 20 世纪 90 年代才开始进行冻土动力学参数的研究. 虽然国内开展冻土动力学参数的研究晚于国外，但通过大量实验，也取得了许多成果.
表 1 显示了国内学者进行冻土动力学参数研究时所采用的方法和实验条件. 表中列出了研究者姓名，在下文图中标注时，用名字拼音的首字母表示，例如，赵淑萍用 ZSP 表示. 表中还列出了所用到的试验土质，主要有粉质黏土、黏土、黄土以及砂土四类，用英文单词的首字母表示，分别为 SC、 C、L、S; 对于土样采集地点，用地名拼音的首字母表示，譬如，青藏黏土用 QZC 表示. 试验方法主要是低温动三轴法和波速法，用 TA、WV 表示. 尽管不同研究者对不同土质、含水量和密度的土样采用不同的试验方法进行试验，但是试验结果具有一定的可比性，而且能找到一些共同的变化规律和特征. 因此，本文在总结、分析国内动力学试验成果的基础上，发现冻土动力学参数的主要特征和变化规律.
2. 1 温度对冻土动力学参数的影响
由于冻土中存在冰，温度变化时会发生冰水相变，因此，温度的变化会对冻土动力学参数产生重要影响.
2. 1. 1 温度对冻土动模量的影响
图 1、图 2 显示了冻土的动弹性模量、动剪切模量随温度的变化曲线. 可以发现如下主要规律:
( 1) 对于相同的土质和试验条件，波速法和动三轴法得到的动模量随温度的变化规律一致，但是，波速法得到的动弹性模量值和动剪切模量值比动三轴法得到的值要大一个量级以上. 对比图 1 ( a) 和( b) 、( d) 和( e) 可见，在 0 ～ - 10 ℃ 的温度范围内，波速法得到的粉质黏土和黄土的动弹性模量在 0 ～ 23 000 MPa 之间变化，而动三轴法得到的动弹性模量在 0 ～ 2 000 MPa 之间变化. 因此，使用时必须根据室内试验条件和模拟工况的对应情况来选择合适的动模量，否则会对计算结果造成很大影响. 波速法试验对应小应变幅、三轴法试验对应中至大应变幅，因此，进行机器振动或车辆振动模拟时，应选择波速法的试验结果; 进行地震模拟时，应选择三轴法的试验结果.
( 2) 冻土的动弹性模量和动剪切模量随温度的变化规律一致，均随温度的降低而增大; 在 0 ～- 5 ℃ 温度范围内，动模量随温度的降低而增大的幅值较大，当温度低于 - 5 ℃ 时，动模量随温度降低而增大的幅值较小. 这是因为冻土中冰的胶结作用对温度变化极为敏感，当温度降低时，冰晶格中氢原子活性减小，冰变为更致密、坚硬的有序结构[43]，冻土的刚性增加，动模量也随之增大，且这种效果在冰水的剧烈相变区 - 5 ～ 0 ℃最明显.
2. 1. 2 温度对冻土泊松比的影响
不同条件下，冻土泊松比随温度的变化关系见图 3. 可以看出，泊松比随着温度的降低而缓慢减小.
2. 1. 3 温度对冻土阻尼比的影响
不同条件下冻土阻尼比随温度的变化曲线见图 4，阻尼比随温度的降低而减小. 在 0 ～ - 5 ℃ 的温度范围内，阻尼比随温度的降低而快速减小，当温 度低于 - 5 ℃后，温度对阻尼比的影响减弱，甚至不再影响其变化. 出现这种变化趋势的原因仍然是 0 ～ - 5 ℃是冰水剧烈相变区，土体性质变化较大，而当温度低于 - 5 ℃后，土体性质变化较小.
2. 2 频率对冻土动力学参数的影响
2. 2. 1 频率对冻土动模量的影响动
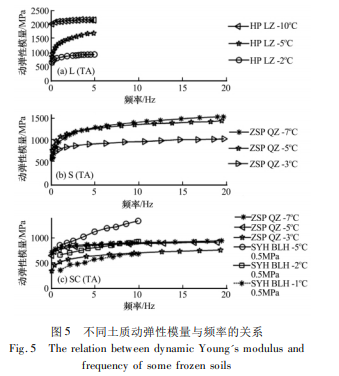
三轴试验可以模拟不同频率的振动荷载. 图 5 显示了不同土质的动弹性模量与振动频率的关系，可以看出，随着荷载振动频率增大，冻土的动弹性模量增大，而且，在较低的频率( 0. 1 ～ 3 Hz) 范围内，动弹性模量随频率增加的幅度较大，而在较高的频率范围( 3 ～ 20 Hz) 内，动弹性模量随频率增加的幅度较小. 这是因为荷载振动频率越高，加荷时间越短，冻土的黏塑性特征来不及体现，因此，表现出较好的弹性性质. 而且，这种时间效应在低频范围内体现得更为明显.
图 6 显示了不同土质动剪切模量与振动频率的关系. 从图中可以看出，粉质黏土的动剪切模量随频率的增大而缓慢增大或基本不变; 黏土的动剪切模量随频率的变化也基本保持不变. 整体来看，动剪切模量随频率的变化幅度小于动弹性模量.
2. 2. 2 频率对冻土阻尼比的影响
从图 7 可以看出，当频率增加时，冻土的阻尼比减小，而且在低频时，变化较大，高频时，变化较小. 但朱占元[20]在 T = - 7 ℃、W = 18. 2% 、σ3 = 0. 5 MPa 的试验条件下测得黏土的阻尼比则随频率的增大而增大. 一般来说，使动模量增加的因素常常会导致阻尼比降低. 譬如，动模量随温度的降低而增加，阻尼比则随温度的降低而降低; 动模量随频率的增加而增加，阻尼比应随频率的增加而减小，图7 中的大多数试验结果符合这个规律. 当然，材料的阻尼本身是比较复杂的，而且各研究者采用的计算方法也不尽一致，因此，阻尼比的变化规律也有可能出现个别的异常，根据实际情况来选用即可.
2. 3 冻土动力学参数随应变幅的变化
2. 3. 1 冻土动模量随应变幅的变化
不同土质的动弹性模量随应变幅的变化过程如图 8 所示. 从图中可以发现黄土、黏土、粉质黏土和高含冰量的粉质黏土的动弹性模量基本上都是随应变幅的增大而减小，而粉砂土的动弹性模量则随应变幅的增大而增大或缓慢增大. 对比图 8( a) 和 ( b) ，可以发现，高含冰量粉质黏土由于其含冰量大、易受温度影响、结构不稳定等因素，导致其动弹性模量远小于粉质黏土.
图 9 是不同土质的动剪切模量和应变幅的关系图，可以发现粉质黏土和黏土的动剪切模量随应变幅的增大而缓慢减小或者基本不变. 整体来看，动剪切模量随应变幅的变化幅度小于动弹性模量.
2. 3. 2 冻土阻尼比随应变幅的变化不同土质阻尼比和应变幅的关系如图 10 所示，从图中可以看出不同土质随应变幅的变化规律不同. 高含冰量粉质黏土阻尼比随应变幅的变化规律性不强. 兰州黄土则有两种情况: 罗飞[30]通过试验得到兰州黄土的阻尼比随应变幅的增大而减小，且在低应变幅时，阻尼比变化幅值较大，在高应变幅时，阻尼比随应变幅的增大开始趋于稳定; 吴志坚等[28 - 29]的试验结果显示兰州黄土的阻尼比随应变幅的增大而增大. 随着应变幅的增大，青藏黏土和粉砂土的阻尼比都是先减小，然后又增大，但是青藏黏土在减小和增大过程中的阻尼比变化幅值明显小于粉砂土. 这里也可以看出，由于材料阻尼的复杂性，加上各研究者的计算方法不一致，即使对于同一种土质，不同学者得到的阻尼比随应变幅的变化规律也不一致，甚至相反. 因此，可以概括地说，冻土的阻尼比随动应变幅变化关系较复杂、规律性不强.
2. 4 含水量对冻土动力学参数的影响土的冻结过程中，土中液态水或水汽相变成固态冰，冰晶或冰层与矿物颗粒在空间上的排列和组合形成冻土的冷生构造[44 - 46]. 土体中含水量越大，在冻结过程中形成的冰晶和冰晶与土颗粒胶结体越多，土体强度发生变化，动力学参数也必然发生变化.
2. 4. 1 含水量对冻土动模量的影响
从图 11 可以看出，不同土质的动弹性模量随含水量的变化趋势一致. 大多数试验结果显示，随着含水量的增大，冻土的动弹性模量先增大后减小，即存在最佳含水量，此时的动弹性模量达到最大，最佳含水量接近于土样的饱和含水量. 这是因为相同温度条件下，随着土体中含水量的增加、冰的含量也增加、冰的胶结作用增强，因此冻土的刚度增加; 当土样含水量超过饱和以后，部分土骨架被撑开、土体的刚度降低，且含水量越大，土骨架被撑开的部分越多，因此，动弹性模量随含水量的增加而降低. 图 11( b) 中施烨辉和马立峰的试验结果显示，当冻结粉质黏土的含水量大于最佳含水量时，动弹性模量降低到一定程度后又开始升高，这是因为随着含水量的进一步增加，冻土变成以冰为主、土颗粒分布其中，动弹性模量取决于冰的含量，含水量越高、冰含量越高、动弹性模量越大.另外，图 11( c) 和( d) 中孟庆洲和王大雁利用波速法测得砂土和黄土的动弹性模量随含水量的增大而线性增大，这可能是因为他们所用的试样含水量范围较小.
图 12 显示了不同土质动剪切模量与含水量的关系，可见，随着含水量的增加，粉质黏土和黏土的动剪切模量都是先增大、后减小或趋于稳定，而黄土和砂土的动剪切模量则一直增大.
2. 4. 2 含水量对冻土泊松比的影响
从图13 可以看出，黄土、黏土和粉质黏土的泊松比都随着含水量的增加而略增大，但是整体的变化幅度较小.
2. 4. 3 含水量对冻土阻尼比的影响
图 14 是不同土质阻尼比和含水量的关系，可以看出阻尼比随含水量的变化呈现出不同的变化趋势. 徐春华等[19]和朱占元[20]的实验结果表明，对于哈尔滨粉质黏土和青藏黏土，随着含水量增大，阻尼比先减小后增大，且相同含水量和温度条件下，围压越大，阻尼比越大; 而赵淑萍[13]试验的粉质黏土和细砂的阻尼比均随着含水量的增加呈缓慢增大的趋势. 可见，冻土阻尼比随含水量的变化规律也不明显.
2. 5 围压对冻土动力学参数的影响
图 15 显示了不同土质动模量随围压的变化.当围压小于 1 MPa 时，冻土的动弹性模量和动剪切模量均随着围压的增加而增加; 围压大于 1 MPa 后，冻土的动剪切模量仍随着围压的增加而增加，但增加速率变缓; 围压大于 1 MPa 后，冻土的动弹性模量随着围压的变化呈现较复杂的趋势，部分试验结果表明，动弹性模量仍随着围压的增加而增加，但增加速率变缓，另一部分试验结果则表明，冻土的动弹性模量随着围压的增加而降低. 这可能是因为围压对冻土动力参数的变化具有双重作用: 一方面，围压使土样受侧向约束，强度提高、刚度变大; 另一方面，高压下孔隙冰将发生局部融化，土颗粒之间产生润滑作用，且冰的流变性随围压的增大呈现增加的趋势最终导致冻土的强度弱化[10]、冻土的刚度也降低. 因此，当围压比较高( 大于 1 MPa) 时，冻土的动弹性模量可能表现出不同的变化趋势.
图 16 是不同土质阻尼比和围压的关系，可以看出，围压变化时，冻土的阻尼比变化也比较复杂，整体上看，冻土阻尼比随着围压的增加呈现增加的趋势.
3 冻土动力学参数的选取和评价
3. 1 冻土动力学参数的选取
目前，国内许多学者对动荷载作用下冻土的动力响应分析进行了数值计算模拟[20 -21，23 -25，32，34 -35，47 -58]，大多数研究者均考虑了冻土的动弹性模量 Ed、动剪切模量 G d、泊松比 μ 和阻尼比 λ 随温度 T 的变化，具体情况如表 2 所示.
3. 2 冻土动力学参数的评价
由于用于数值模拟的冻土动力学参数源数据来自于室内低温动三轴试验，所以对比表 3 和表 4 可以发现，李双洋等[47]应用于数值模拟的亚黏土动弹性模量预估值小于试验值; 常立武等[55 - 56]应用于数值模拟的粉质黏土的动弹性模量预估值和试验值比较接近
相关知识推荐：地质勘查专业刊物有哪些
.表 5 是 利 用 式 ( 8 ) 、( 10 ) 计 算 的 - 0. 5 ～- 20 ℃ 温度范围内泊松比的预估值. 对比表 6 可知，在相同的温度范围内，利用李双洋等[47]的预估模型得到亚黏土的泊松比预估值的波动范围小于试验值; 利用常立武等[55 - 56]的预估模型得到的预估值远大于试验值.
3. 3 冻土动力学参数的选取建议
应用于数值计算中的冻土动力学参数的获取基本上都是采用一段式线性关系公式求得，如式( 7) 、 ( 9) ，但是从图 1 和图 2 中可以明显看出，动弹性模量和动剪切模量的变化趋势并非一段式的线性关系. 在 - 5 ℃左右，动弹性模量和动剪切模量随温度的变化率出现较大变化，当温度高于 - 5 ℃ 时，动弹性模量和动剪切模量随温度的降低而急剧增大; 当温度低于 - 5 ℃ 时，动弹性模量和动剪切模量随温度的降低而缓慢增大，所以，建议以 - 5 ℃ 为分界点，动弹性模量和动剪切模量的预估模型采用两段式线性关系，如: Ed1 = a1T + b1 ( - 5 ℃ < T < 0 ℃ ) ( 11) Ed2 = a2T + b2 ( T < - 5 ℃ ) ( 12) 式中: a1、a2、b 1、b 2为试验常数; T 为温度.对于列车荷载振动，由于列车作用在铁轨上的振动传播需要经过道砟，路基填土等才会传递到冻土层，而此时的振动应变幅已经很小，冻土振动响应的应变幅达不到低温动三轴法所要求的大应变幅，所以用动三轴法获取的冻土动力学参数不仅不适合应用于数值模拟，而且也不适用于对寒区道路工程的稳定性进行预测和评价，建议在进行列车荷载作用下冻土路基的响应分析时选用波速法的试验结果.
4 结论
本文在总结、分析国内动力学试验成果的基础上，发现冻土动力学参数的主要特征和变化规律，并进一步给出动力学参数选取的建议.
( 1) 对于相同的土质和试验条件，波速法和动三轴法得到的动模量随温度的变化规律一致，但是，波速法得到的动弹性模量值和动剪切模量值比动三轴法得到的值要大一个数量级以上.
( 2) 冻土的动弹性模量和动剪切模量随温度的变化规律一致，均随温度的降低而增加; 在 0 ～- 5 ℃ 的温度范围内，动模量随温度的降低而增大的幅值较大，当温度低于 - 5 ℃ 时，动模量随温度降低而增大的幅值较小.
( 3) 随着荷载振动频率增大，冻土的动弹性模量增大，而且，在较低的频率( 0. 1 ～ 3 Hz) 范围内，动弹性模量随频率增加的幅度较大，而在较高的频率范围( 3 ～ 20 Hz) 内，动弹性模量随频率增加的幅度较小. 冻土的动剪切模量也随着频率的增加而增加，但是，整体来看，动剪切模量随频率的变化幅度小于动弹性模量的.
(4) 黄土、黏土、粉质黏土和高含冰量的粉质黏土的动弹性模量基本上都是随应变幅的增大而减小，而粉砂土的动弹性模量则随应变幅的增大而增大或缓慢增大. 粉质黏土和黏土的动剪切模量随应变幅的增大而缓慢减小或者基本不变. 整体来看，动剪切模量随应变幅的变化幅度小于动弹性模量的.
( 5) 随着含水量的增大，冻土的动弹性模量先增大后减小，即存在最佳含水量，此时的动弹性模量达到最大; 粉质黏土和黏土的动剪切模量都是先增大、后减小或趋于稳定，而黄土和砂土的动剪切模量则一直增大.
( 6) 当围压小于 1 MPa 时，冻土的动弹性模量和动剪切模量均随着围压的增加而增加.
( 7) 冻土的泊松比随着温度的降低而缓慢减小. 在 0 ～ - 5 ℃ 的温度范围内，阻尼比随温度的降低而快速减小，当温度低于 - 5 ℃ 后，温度对阻尼比的影响减弱，甚至不再影响其变化.
( 8) 阻尼比随频率、应变幅、含水量和围压的变化比较复杂、规律性不强.
( 9) 建议采用两段式线性模型来预估冻土的动模量随温度变化的关系，以 - 5 ℃ 作为两段式的分界点.
( 10) 波速法试验对应小应变幅、三轴法试验对应中至大应变幅，因此，进行机器振动或车辆振动模拟时，建议选择波速法的试验结果，进行地震模拟时，建议选择三轴法的试验结果.
5 展望
通过对国内冻土动力学参数研究的现状进行论述，可以发现，目前，室内测试技术日趋成熟，动力学参数资料也较丰富，但是现场测试数据和实际应用却很少，所以还需要在以下几个方面进一步开展深入研究: ( 1) 开展冻土动力学参数现场原位测试，以便冻土动力学参数的研究成果能更好地应用于工程实践; ( 2) 由于冻土结构的复杂性，加上动荷载的复杂性，使冻土的动本构关系难以确定，普通土动力学模型不能完全应用于冻土，所以需要利用室内试验和现场原位测试获得的冻土动力学参数来进一步改进普通土动力学模型，以更好地模拟冻土的实际情况; ( 3) 把冻土动力学参数、计算模型和数值模拟结合起来，预测动荷载作用下冻土的动力响应，更好地服务于工程建设. 总之，须进一步将室内试验、现场原位试验、模型试验和实际工程检测紧密结合，从而不断发展和完善冻土在动荷载作用下响应分析理论，并将其应用于工程实践中.——论文作者：肖东辉1，2 ， 马 巍1 ， 赵淑萍3* ， 张 泽1 ， 蔡 聪1，2
参考文献( References) :
[1] Cheng Guodong，Yang Chengsong. Mechanics related with frozen ground in construction of Qinghai-Tibet Railway[J]. Mechanics and Engineering，2006，28( 3) : 1 - 8. [程国栋，杨成松. 青藏 铁 路 建 设 中 的 冻 土 力 学 问 题[J]. 力 学 与 实 践， 2006，28( 3) : 1 - 8.]
[2] Zhu Zhanyuan，Li Jing，Zou Zuyin，et al. Study on deformation characters of frozen soil under load-term dynamic loading[J]. Low Temperature Architecture Technology，2008 ( 2 ) : 112 - 114. [朱占元，李静，皱祖银，等. 动力荷载作用下冻土变形特性研究[J]. 低温建筑技术，2008( 2) : 112 - 114.]
[3] Zheng Yun，Ma Wei，Bing Hui. Impact of freezing and thawing cycles on the structures of soil and a quantitative approach[J]. Journal of Glaciology and Geocryology，2015，37 ( 1 ) : 132 - 137. [郑郧，马巍，邴慧. 冻融循环对土结构性影响的机理与定量研究方法[J]. 冰川冻土，2015，37( 1) : 132 - 137.]
[4] Cai Zhengyin，Wu Zhiqiang，Huang Yinghao，et al. Experimental study on the factors influencing the uniaxial compressive strength of frozen soil[J]. Journal of Glaciology and Geocryology，2015，37( 4) : 1002 - 1008. [蔡正银，吴志强，黄英豪，等. 冻土单轴抗压强度影响因素的试验研究[J]. 冰川冻土， 2015，37( 4) : 1002 - 1008.]
[5] Vinson T S. Response of frozen ground to dynamic loadings [M]/ /Geotechnical engineering in cold regions. New York: McGraw -Hill Book Company，1978: 405 - 458.
[6] Vinson T S，Li J C. Dynamic properties of frozen sand under simulated earthquake loading conditions[C]/ /Proceedings of the 7th World Conference on Earthquake Engineering. Istanbul，Turkey: Turkish National Committee on Earthquake Engineering， 1980: 225 - 240.
[7] Vinson T S，Wilson C R，Bolande R P. Dynamic properties of naturally frozen silt[C]/ /Proceedings of 4th International Conference on Permafrost. Washington，D. C. : National Academy Press，1983: 469 - 481.
[8] Czajkow ski R L，Vinson T S. Dynamic properties of frozen silt under cyclic loading[J]. Journal of the Geotechnical Engineering Division，1980，106( 9) : 963 - 980.
[9] Li J C，Baladi G Y，Andersland O B. Cyclic triaxial tests on frozen sand[J]. Engineering Geology，1979，13 ( 2 ) : 233 - 246.
[10]Ma Wei，Wang Dayan. Mechanics of frozen soil[M]. Beijing: Science Press，2014. [马巍，王大雁. 冻土力学[M]. 北京: 科学出版社，2014.]
SCI SSCI AHCI