0
留言稍后联系!

发布时间:2022-02-10所属分类:电工职称论文浏览:1730次
摘 要: 摘要: 风力发电和电锅炉等电采暖负荷接入配电网的可靠性评估过程中,风速-负荷联合二元正态分布函数不能够反映风速-电锅炉等电采暖负荷之间的相关性,从而影响了计算的准确性。基于 Copula 理论,建立风速-电锅炉等电采暖负荷相关性的 Gumbel-Copula 函数关系,通过极

摘要: 风力发电和电锅炉等电采暖负荷接入配电网的可靠性评估过程中,风速-负荷联合二元正态分布函数不能够反映风速-电锅炉等电采暖负荷之间的相关性,从而影响了计算的准确性。基于 Copula 理论,建立风速-电锅炉等电采暖负荷相关性的 Gumbel-Copula 函数关系,通过极大似然估计确定 Copula 函数中的具体参数,得到其联合概率密度分布函数,并利用蒙特卡洛模拟法计算配电网可靠性指标。通过算例分析结果表明,Gumbel-Copula 函数能够较好地反映风速和电锅炉等电采暖负荷之间的相关性,基于所提模型可有效、准确地计算风电和电采暖负荷接入配电网的可靠性。
关键词: 配电网; 可靠性评估; Copula 理论; 电采暖负荷; 蒙特卡洛方法
0 引言
“以电代煤、以电代油、电从远方来”为核心的电能替代工作主要集中在配电网,当前电能替代的主要领域是电采暖,其通常被安排在低谷电价的夜间运行,导致夜间负荷大幅度增加,而通常风速在夜间较大,使风力发电机在夜间产生更大的电能。风力发电与电采暖负荷具有较大的相关性[1],基于二者相关性分析的可靠性评估,有助于更加准确地计算配电网的可靠性指标。
传统的配电网可靠性评估方法缺乏考虑分布式电源出力的随机性[2-4],文献[5-9]研究了含分布式电源的配电网可靠性评估方法,虽然考虑了分布式电源出力的随机性,但通常假定负荷不变,其评估结果偏于保守。为了准确计算含分布式电源的配电网可靠性指标,文献[10-12]考虑了分布式电源和负荷的随机性。文献[10]分别模拟 4 种季节下一天的典型时序负荷曲线和风速曲线,并用蒙特卡洛模拟法计算系统的可靠性指标,在一定程度上提高了可靠性指标计算的准确性;文献[11]在计算含储能装置的风电系统接入配电网运行的可靠性指标时,考虑了风速和负荷变化的影响,用蒙特卡洛模拟法对时序负荷进行抽样,分别计算与不同负荷对应的系统可靠性指标,并比较 3 种储能策略对系统可靠性的影响;文献[12]在对风速进行自回归滑动平均(ARMA)预测时,考虑了与负荷相关的温度变化对风速的影响,采用非参数估计的方法得到含温度参量的时序风速,相较于文献[10-11],其以温度为桥梁间接考虑了风速-负荷之间的相关性,但仍没有直接研究二者之间的相关性。为此,文献[13]利用多元统计方法建立风速-负荷的正态分布模型,计算二者的相关系数,得到风速-负荷联合二元正态分布函数,用蒙特卡洛模拟法对风速-负荷序列进行抽样,计算系统可靠性指标,其假定风速和负荷都是服从正态分布,而且风速-负荷之间线性相关,但统计数据表明,实际的风速大多服从威布尔分布[14],负荷也非严格地服从正态分布,因此简单地假定风速和负荷均服从正态分布的可靠性评估结果可能相对保守。
为此,本文采用能够连接各种边缘分布函数的 Copula 函数[15]形成风速-电锅炉等电采暖负荷的联合分布函数,从而在配电网可靠性评估中考虑风速电锅炉等电采暖负荷之间的相关性。
1 风速和电锅炉等电采暖负荷边缘分布及相关性分析
1.1 风速和电锅炉等电采暖负荷的边缘分布
1.1.1 风速的边缘分布
目前,相较于正态分布[16]和瑞利分布[17],双参数的威布尔分布曲线普遍被认为是适用于风速统计描述的概率函数,威布尔分布函数的概率密度函数如下:
1.1.2 电锅炉等电采暖负荷的边缘分布
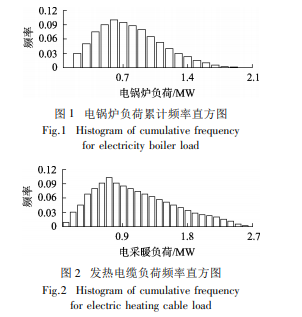
电锅炉等电采暖负荷的边缘分布可参考累计频率直方图,当前电采暖的主要方式是集中式供暖的电锅炉和分散式供暖的发热电缆。图 1 和图 2 分别给出了乌鲁木齐市 2016 年某馈线上 1 台电锅炉采暖和 1 个发热电缆采暖的电采暖负荷的累计频率直方图。
由图 1 和图 2 可以看出,电锅炉和发热电缆负荷概率分布曲线与威布尔分布曲线最相似,电锅炉和发热电缆负荷与风速一样,预测服从威布尔分布。
1.2 风速-电锅炉等电采暖负荷相关性分析
为了分析风速-电锅炉等电采暖负荷的相关性,以 2016 年乌鲁木齐市的一条馈线为例,该馈线上有 2 台风机、1 个电锅炉负荷、1 个发热电缆负荷,其余为常规负荷。图 3 给出了乌鲁木齐市风速、电锅炉负荷、发热电缆负荷和常规负荷 24 h 平 均 负 荷曲线。
在图 3 中,为了加大曲线的区分度,风速取原有风速的 1 /10,考虑到只是比较各曲线的变化趋势,以上处理是合理的。电锅炉、发热电缆负荷曲线和风速曲线都是凹型,说明它们相关程度较高,但风速下降和上升过程斜率较大,而电锅炉和发热电缆负荷变化斜率较小,说明风速和电锅炉、发热电缆负荷不是线性相关;常规负荷是双峰曲线,与风速曲线相关程度低。
文献[15]指出,只有联合分布服从对称的椭圆分布,如二元正态分布、t 分布,且当变量之间为线性相关时,联合概率分布函数才能由变量间的相关系数和边缘分布唯一确定,而风速、电锅炉负荷和发热电缆负荷都服从威布尔分布,相关系数也不是线性相关。因此文献[13]提出的风速-负荷服从正态分布,且二者线性相关条件下形成的联合分布函数已不在适用,需采用非线性相关分析工具 Copula 理论构建风速-电锅炉负荷和风速-发热电缆负荷的联合分布函数,提高配电网可靠性评估结果的准确性。
2 基于 Copula 理论的风速-电锅炉等电采暖负荷联合分布函数
2.1 Copula 理论简介
通常很难直接给出多元随机变量的联合概率分布函数,而 Copula 函数[15]是一个将多元随机变量的联合概率分布表示为各自边缘分布的连接,是构建多元相关随机变量联合分布的有力工具。
2.2 Copula 函数的选择及参数估计
根据表 1 可知,不同的 Copula 函数类型有不同的特性,选取 Copula 函数类型的最直接的方法是画出风速-电锅炉等电采暖负荷的散点图或二元直方图,根据图形特性选择 Copula 函数。
选取收集的乌鲁木齐某馈线 2016 年实测数据进行分析,该馈线上有 2 台 1.5 MW 的风机,分布在不同的节点上,有 1 个电锅炉和发热电缆的电采暖负荷。图 4 和图 5 分别给出了 2 个典型的风速-电锅炉负荷、风速-发热电缆负荷的数值转换到[0,1]区间的散点图。经观察可知,风速-电锅炉负荷、风速-发热电缆负荷之间的相关性具有非对称的上后尾特性。实测数据证明风速-电锅炉负荷和风速发热电缆负荷有较强的相关性,尤其是在风速较大的夜晚,电力公司通过低谷电价鼓励蓄热式电锅炉用电。
因此,基于图 4 和图 5,对于风速-电锅炉负荷和风速-发热电缆负荷的 Copula 函数的确定,就不必与文献[14]类似,先计算表 1 中的 5 类 Copula 函数,然后通过拟合优度检验确定最优的 Copula 函数,而是基于后尾特性直接选择 Gumbel-Copula 模型。
3.2 配电网可靠性评估方法
计及风速-电锅炉等电采暖负荷相关性的配电网可靠性评估方法如下:
a. 依据现有采样的数据,利用灰色模型估算风速、电锅炉和发热电缆负荷的威布尔分布参数,利用一步估计法分别估算风速-电锅炉和风速-发热电缆的 Copula 函数参数;
b. 利用蒙特卡洛模拟法从风速-电锅炉负荷、风速-发热电缆负荷 Copula 函数中分别抽取 n 组随机变量(Fwi,Fei),其中 i = 1,2,…,n;
c. 对随机变量(Fwi,Fei)进行累积分布逆变换,产生随机的风速和电锅炉、发热电缆负荷值,生成 n 个服从联合分布 Copula 函数的场景;
d. 在常规负荷服从正态分布的条件下,利用最大似然估计法[20]确定均值和方差,再利用蒙特卡洛模拟法模拟产生 n 组常规负荷的随机变量;
e. 依据开关装置位置将配电网分块,根据风速计算的风机出力值,采用广度优先搜索算法,从风机节点开始由近到远确定 n 组风机的供电范围,但是考虑到系统分块的特点,风机供电范围按照块确定;
f. 按照式(7)—(13)计算每组数据的可靠性指标,取 n 组可靠性指标的平均值,得到考虑风速-电锅炉负荷和风速-发热电缆负荷相关性的配电网可靠性指标。
4 算例分析
4.1 算例介绍
以乌鲁木齐市 85 节点系统中某条馈线及其 2016 年的数据为例进行分析,馈线系统图见附录中图 A1。该馈线有 2 台 1.5 MW 的风机(1 号风机连接在节点 14,2 号风机连接在节点 75)、7 个连接馈线段的分段开关、2 个连接风机的分段开关;节点 15 上为电锅炉负荷,节点 17 上为发热电缆负荷,其余节点为常规负荷。表 2 和表 3 分别给出各设备的可靠性系数和负荷块包含的负荷点数据。
4.2 相关性分析
根据 2016 年 1 号风机和 2 号风机的历史风速数据、电锅炉和发热电缆负荷的历史数据,进行威布尔分布拟合校核,得到相应的形状参数和尺度参数如表 4 所示。
表 5 给出了风机风速-电锅炉负荷和风机风速发热电缆负荷联合概率密度函数的相依参数 α 的估算值。
根据表 5 可知,相依参数均大于 3,表明风速-电锅炉负荷和风速-发热电缆负荷具有很好的相关性; 2 号风机风速-电锅炉负荷和 1 号风机风速-发热电缆负荷的相关性更大。
4.3 配电网可靠性评估
为了分析风速-电锅炉负荷和风速-发热电缆负荷相关性对可靠性评估的影响,基于 2016 年历史数据,去掉坏数据,实际的场景数是 25 315 个,因此蒙特卡洛模拟法也抽取 25 315 组数据。表 6 给出了不计及相关性、文献[13]方法(风速和负荷都是服从正态分布,风速-负荷联合分布函数为二元正态分布函数)、本文方法和实际数据计算得到的可靠性指标。
由表 6 可知,相比于不计及相关性,文献[13]方法的计算结果更接近实际值,而本文方法比文献[13]的结果更接近实际值,系统平均停电频率指标 SAIFI 和系统平均停运持续时间指标 SAIDI 得到明显的降低,更接近实际计算值,平均供电可用率指标 ASAI 得到了提高,系统缺电量 ENS 也减少了,系统的可靠性指标得到明显的改善,更接近实际值,说明不计及风速-电锅炉负荷和风速-发热电缆负荷相关性以及文献[13]的风速-负荷联合分布函数为二元正态分布函数,计算的可靠性评估结果相对保守。
5 结论
本文基于 Copula 理论研究了计及风速-电锅炉等电采暖负荷相关性的配电网可靠性评估。通过计算乌鲁木齐市某馈线风速-电锅炉等电采暖负荷相关性分析和可靠性评估结果,可得出如下结论:
a. 相比于常规负荷服从正态分布,电锅炉等电采暖负荷通常服从威布尔分布;
b. 风速-电锅炉等电采暖负荷之间的相关性具有非对称的上后尾特性,它们之间的 Copula 函数可选择 Gumbel-Copula 函数,算例分析中该函数的相依参数值较大,表明它们之间具有较大的相关性;
c. 相比于不计及相关性、考虑风速-负荷联合分布函数为二元正态分布函数的配电网可靠性评估结果,本文所提的考虑风速、电锅炉等电采暖负荷实际边缘分布,基于 Copula 函数的计及风速-电锅炉等电采暖负荷相关性的配电网可靠性评估结果更接近实际值。——论文作者:李 娟1 ,周红莲1 ,周二彪1 ,刘自发2 ,王 威3
参考文献:
[1]路晓敏,陈磊,徐飞,等. 电热综合能源系统框架下蒙西电网电源容量最 优 配 比 研 究[J]. 电力自动化设备,2017,37 ( 6): 132-138. LU Xiaomin,CHEN Lei,XU Fei,et al. Optimal energy-source capacity ratios of integrated electricity-heat energy system of West Inner Mongolia Power Grid[J]. Electric Power Automation Equipment,2017,37(6):132-138.
[2]张鹏,王守相. 大规模配电系统可靠性评估的区间算法[J]. 中国电机工程学报,2004,24(3):77-84. ZHANG Peng,WANG Shouxiang. A novel interval method for reliability evaluation of large scale distribution system[J]. Proceedings of the CSEE,2004,24(3):77-84.
[3]赵洪山,赵航宇,侯杰群,等. 需求响应对配电网供电可靠性影响分析[J].电力自动化设备,2017,37(1):8-14. ZHAO Hongshan,ZHAO Hangyu,HOU Jiequn,et al. Effect of demand response on supply reliability of distribution network[J]. Electric Power Automation Equipment,2017,37(1):8-14.
[4]蒋卓臻,刘俊勇,向月. 配电网信息物理系统可靠性评估关键技术探讨[J]. 电力自动化设备,2017,37(12):30-42. JIANG Zhuozhen,LIU Junyong,XIANG Yue. Key technologies for reliability assessment of distribution network cyber physical system [J]. Electric Power Automation Equipment,2017,37(12):30-42.
[5]BAE I S,KIM J O. Reliability evaluation of distributed generation based on operation mode[J]. IEEE Transactions on Power Systems,2007,22(2):785-790.
[6]SASAKI Y,KITA H,TANAKA E. Evaluation of cost and reliability of power systems with large numbers of distributed generators[J]. Electrical Engineering in Japan,2009,167(2):28-37.
[7]姜文,严正. 含风电场的发输电组合系统可靠性评估[J]. 电力自动化设备,2010,30(4):5-9. JIANG Wen,YAN Zheng. Reliability assessment of composite generation and transmission system with wind farms[J]. Electric Power Automation Equipment,2010,30(4):5-9.
[8]王韶,谭文,黄晗. 计及微电网中可再生能源间歇性影响的配电网可靠性评估[J]. 电力自动化设备,2015,35(4):31-37. WANG Shao,TAN Wen,HUANG Han. Distribution system relidability evaluation considering influence of intermittent renewable energy sources for microgrid[J]. Electric Power Automation Equipment,2015,35(4):31-37.
[9]赵渊,何媛,宿晓岚,等. 分布式电源对配网可靠性的影响及优化配置[J]. 电力自动化设备,2014,34(9):13-20. ZHAO Yuan,HE Yuan,SU Xiaolan,et al. Effect of distributed generation on power distribution system reliability and its optimal allocation[J]. Electric Power Automation Equipment,2014,34 ( 9): 13-20.
[10]JAYAWEERA D,ISLAM S. Probabilistic assessment of distribution network capacity for wind power generation integration[C]∥2009 Australasian Universities Power Engineering Conference(AUPEC). Adelaide,SA,Australia:IEEE,2009:1-6.
[11]BHUIYAN F A,YAZDANI A. Reliability assessment of a wind-power system with integrated energy storage[J]. IET Renewable Power Generation,2010,4(3):211-220.
[12]CALLAWAY D S. Sequential reliability forecasting for wind energy temperature dependence and probability distributions[J]. IEEE Transactions on Energy Conversion,2010,25(2):577-585.
[13]孙若笛,谢开贵. 计及风速-负荷相关性的配电网可靠性评估 Monte Carlo 模拟法[J]. 电力系统保护与控制,2012,40( 18): 12-18. SUN Ruodi,XIE Kaigui. Reliability evaluation of distribution networks using Monte Carlo method considering correlations between wind speed and load[J]. Power System Protection and Control, 2012,40(18):12-18.
澹版槑:鈶犳枃鐚潵鑷煡缃戙€佺淮鏅€佷竾鏂圭瓑妫€绱㈡暟鎹簱锛岃鏄庢湰鏂囩尞宸茬粡鍙戣〃瑙佸垔锛屾伃鍠滀綔鑰�.鈶″鏋滄偍鏄綔鑰呬笖涓嶆兂鏈钩鍙板睍绀烘枃鐚俊鎭�,鍙仈绯�瀛︽湳椤鹃棶浜堜互鍒犻櫎.
SCISSCIAHCI